Programma del
corso di
"
MECCANICA RAZIONALE"
Corso di Laurea
in Ingegneria Meccanica - A.A. 1999-00
2°Anno, 2°Semestre
Docente:
Prof. GIOVANNI FROSALI
INTRODUZIONE.
Che cos'è la Meccanica Razionale. I
fenomeni fisici ed i loro modelli. Esempi. F = m a
ed i sistemi dinamici. Analogia fra un fenomeno meccanico ed uno
elettrico. Primo esempio: oscillatore forzato e circuito LRC.
Cosa si intende per modello matematico. Le grandezze della
meccanica: scalari, vettoriali e tensoriali. Sistema
internazionale di misura.
ELEMENTI DI CALCOLO VETTORIALE.
Vettori geometrici e rappresentazione
di grandezze vettoriali con vettori geometrici. Cenni riassuntivi
di calcolo vettoriale e notazioni. Rappresentazione cartesiana.
Prodotto scalare e vettoriale. Prodotto misto e doppio prodotto
vettoriale. Cambiamento di riferimento. Punti e vettori funzioni
di un parametro. Vettori funzione del posto. Derivazione ed
integrazione.
TEORIA DEI MOMENTI.
Momento polare e momento assiale.
Sistemi di vettori applicati e coppia di vettori applicati.
Momento risultante di un sistema di vettori applicati. Variazione
del momento al variare del centro di riduzione. Coppia di
vettori. Invariante scalare e vettoriale. Esistenza dell'asse
centrale. Soluzione di a = x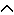 b e discussione. Ricerca analitica dell'asse
centrale. Equazione dell'asse centrale. Caso Mp = 0.
Sistemi di vettori applicati concorrenti, paralleli, complanari.
Teorema di Varignon. Sistemi equivalenti, sistemi equilibrati.
Sistemi di vettori riducibili al solo risultante applicato
sull'asse centrale. Rappresentazione del campo vettoriale dei
momenti. Vettori paralleli, centro di vettori paralleli. Esercizi
di calcolo di asse centrale per alcuni sistemi di vettori.
b e discussione. Ricerca analitica dell'asse
centrale. Equazione dell'asse centrale. Caso Mp = 0.
Sistemi di vettori applicati concorrenti, paralleli, complanari.
Teorema di Varignon. Sistemi equivalenti, sistemi equilibrati.
Sistemi di vettori riducibili al solo risultante applicato
sull'asse centrale. Rappresentazione del campo vettoriale dei
momenti. Vettori paralleli, centro di vettori paralleli. Esercizi
di calcolo di asse centrale per alcuni sistemi di vettori.
ELEMENTI DI STATICA DEL CORPO RIGIDO. Sistemi rigidi
liberi e vincolati. Equazioni cardinali della statica. Sistemi
materiali piani. Esempi. Principali tipi di vincolo nel piano.
Appogio semplice, cerniera, incastro, pattino. Posizione del
problema statico: problemi labile, isostatico, iperstatico.
Sistemi staticamente determinati. Vincoli efficaci. Alcuni esempi
di sistemi piani. Problemi di statica per sistemi formati da un
solo corpo rigido. Problemi di statica per sistemi formati da
più parti rigide. Arco a tre cerniere. Cenni di statica grafica.
Poligono funicolare. Osservazioni sul poligono funicolare.
Condizione grafiche per l'equilibrio. Alcuni esempi di
risoluzione grafica: trave orizzontale ed obliqua, trave
incastrata, arco a tre cerniere.Teorema di Culmann
ed applicazioni.
CINEMATICA DEL PUNTO.
Il problema fondamentale della cinematica del punto.
Equazioni differenziali di moto. Integrali primi di moto.
Elementi di geometria differenziale nello spazio. Richiami di
elementi della teoria delle curve. Il triedro principale,
curvatura. Calcolo di t,n,b. Esempi:
circonferenza, parabola, elica cilindrica. Moti piani. Velocità
e accelerazione in coordinate polari, sferiche e cilindriche.
Composizione di moti. Moti centrali. Proprietà dei moti
centrali. Velocità areolare. Costanza della velocità areolare e
conseguenze. Moto circolare. Esercizi di cinematica del punto.
Ricerca di legge oraria e traiettoria.
SISTEMI RIGIDI.
Definizione di sistema rigido. Gradi di libertà. Gli
angoli di Eulero. Sistemi rigidi vincolati all'esterno,
particolari vincoli esterni: appoggio, cerniera cilindrica e
sferica, incastro. Sistemi costituiti da parti rigide collegate
tra loro. Sistemi isostatici e iperstatici, sistemi staticamente
determinati. Condizioni grafiche per l'equilibrio di un sistema
piano di forze applicate: chiusura del poligono delle forze e del
poligono funicolare. Analisi esterna ed analisi interna per un
sistema rigido: sforzo normale, sforzo di taglio, momente
flettente e momento torcente. Caso dei sistemi piani. Semplici
applicazioni alle travi.
CINEMATICA DEI SISTEMI RIGIDI.
Sistemi di riferimento fisso e solidale.
Trasformazioni lineari ortogonali. Trasformazione del piano in
sé. Rotazioni nel piano. Richiami di calcolo matriciale. Moti
rigidi. Formule di Poisson. Esistenza e unicità di 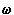 .
Espressione di
.
Espressione di 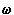 in funzione di una coordinata angolare.
Relazione fondamentale tra le velocità simultanee di due punti.
Velocità ed accelerazione dei punti di un sistema rigido in
moto. Asse istantaneo di moto, sua esistenza e ricerca analitica.
Rigata fissa e rigata mobile. Rigate di un moto rigido. Esempio:
rotolamento senza e con strisciamento di un disco su una guida
rettilinea. Moti rigidi particolari: traslazioni, rotazioni,
precessioni. Moto rototraslatorio. Moti rigidi piani. Polari di
un moto rigido piano. Centro istantaneo di moto nei moti rigidi
piani. Teorema di Chasles. Esempi di moto rigido piano. Moto di
una asta rigida con gli estremi su due guide ortogonali. Ricerca
del centro istantaneo di moto e delle polari di moto. Centro
delle accelerazioni, circonferenza dei flessi e circonferenza di
stazionarietà. Diagramma delle accelerazioni Cenni sulle matrici
ortogonali (autovalore 1). Teorema di Eulero. Rotazioni finite e
infinitesime. Matrici antisimmetriche e rotazioni infinitesime.
in funzione di una coordinata angolare.
Relazione fondamentale tra le velocità simultanee di due punti.
Velocità ed accelerazione dei punti di un sistema rigido in
moto. Asse istantaneo di moto, sua esistenza e ricerca analitica.
Rigata fissa e rigata mobile. Rigate di un moto rigido. Esempio:
rotolamento senza e con strisciamento di un disco su una guida
rettilinea. Moti rigidi particolari: traslazioni, rotazioni,
precessioni. Moto rototraslatorio. Moti rigidi piani. Polari di
un moto rigido piano. Centro istantaneo di moto nei moti rigidi
piani. Teorema di Chasles. Esempi di moto rigido piano. Moto di
una asta rigida con gli estremi su due guide ortogonali. Ricerca
del centro istantaneo di moto e delle polari di moto. Centro
delle accelerazioni, circonferenza dei flessi e circonferenza di
stazionarietà. Diagramma delle accelerazioni Cenni sulle matrici
ortogonali (autovalore 1). Teorema di Eulero. Rotazioni finite e
infinitesime. Matrici antisimmetriche e rotazioni infinitesime. 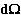 come pseudovettore. Asse ed angolo di rotazione. Richiami di
cinematica relativa. Moto relativo e moto di trascinamento.
Teorema fondamentale della cinematica relativa. Teorema di
Coriolis. Derivata assoluta e relativa. Moto uniforme di un punto
su una guida ruotante. Esempi per mostrare l'effetto della
accelerazione di Coriolis. Esercizi sui moti relativi.
Composizione di moti. Composizione di moti rigidi. Composizione
di rotazioni. Moti epicicloidali e ipocicloidali. L'esempio del
differenziale.
come pseudovettore. Asse ed angolo di rotazione. Richiami di
cinematica relativa. Moto relativo e moto di trascinamento.
Teorema fondamentale della cinematica relativa. Teorema di
Coriolis. Derivata assoluta e relativa. Moto uniforme di un punto
su una guida ruotante. Esempi per mostrare l'effetto della
accelerazione di Coriolis. Esercizi sui moti relativi.
Composizione di moti. Composizione di moti rigidi. Composizione
di rotazioni. Moti epicicloidali e ipocicloidali. L'esempio del
differenziale.
DINAMICA DEL PUNTO MATERIALE LIBERO E
VINCOLATO.
Sistemi di riferimento. Sistema inerziale e postulato
della sua esistenza. Le leggi di Newton. Equazioni di moto dei
sistemi materiali isolati. Il principio di relatività
galileiana. Sistemi non inerziali. Derivata assoluta e relativa.
Dinamica relativa. Equazioni di moto in un riferimento non
inerziale. Il peso. Esercizi di dinamica relativa.
QUESTIONI GENERALI DI DINAMICA DEL PUNTO.
Lavoro e potenza. Teorema delle forze vive e integrale
delle forze vive. Forze conservative. Energia totale.
Conservazione dell'energia totale. Calcolo di lavoro. Forme
differenziali esatte e chiuse. Primitiva di una forma
differenziale. Condizioni sufficienti per l'esattezza. Calcolo
del potenziale nei campi conservativi. Campi di forza. Linee di
forza. Differenza fra traiettoria e linea di forza. Esercizi di
calcolo di linee di forza. Calcolo di lavoro (integrali
curvilinei). Forme differenziali esatte e chiuse. Condizioni
sufficienti per l'esattezza. Calcolo del potenziale nei campi
conservativi. Primitiva di una forma differenziale. Esercizi di
calcolo di potenziale. Il campo di Biot-Savart, generato dal
passaggio di una corrente in un filo rettilineo indefinito.
Potenziale in coordinate cartesiane e cilindriche. Calcolo di
lavoro in un campo non conservativo. Campi centrali. Richiami di
calcolo differenziale. Derivata parziale e gradiente. Funzioni
differenziali e rappresentazione lineare. Campi scalari e
vettoriali. grad, div, rot: definizioni e
proprietà. Significato di gradiente di un campo scalare.
Significato di rotore. Rappresentazione in coordinate cartesiane
del gradiente: Operatore 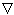 . Divergenza e rotore di un
campo vettoriale. Flusso di un campo e teorema della divergenza.
. Divergenza e rotore di un
campo vettoriale. Flusso di un campo e teorema della divergenza.
MOTI OSCILLATORI.
Fase ed ampiezza di una oscillazione. Uso dei numeri
complessi. Gli esponenziali complessi. Vettori rotanti. Moto
armonico. Composizione di due moti armonici su una retta con lo
stesso centro. Accordo di fase, opposizione di fase, quadratura
di fase. Modulazione armonica dell'oscillazione fondamentale. Il
fenomeno dei battimenti. Composizione di due moti armonici,
aventi lo stesso centro, su assi ortogonali (figure di
Lissajous). Composizione di oscillazioni con l'uso degli
esponenziali complessi. Oscillazioni libere unidimensionali.
Oscillatore lineare con termine forzante. Soluzioni di equazioni
differenziali del secondo ordine col formalismo dei numeri
complessi. Oscillatore smorzato. Moto oscillatorio smorzato, moto
non oscillatorio. Analogie elettriche: circuito LRC in serie.
Oscillazioni forzate. Vibrazioni armoniche permanenti. Diagramma
del ritardo di fase. Risonanza e curve di risonanza. Analogie
elettriche: scarica di un condensatore su una bobina con e senza
resistenza. Circuito LRC in serie con d.d.p. applicata.
APPLICAZIONI DELLA LEGGE FONDAMENTALE DELLA
DINAMICA DI UN PUNTO MATERIALE.
Lancio di un grave nel vuoto. Gittata massima e
parabola di sicurezza di Torricelli. Resistenza nei mezzi.
Resistenza lineare (viscosa) e quadratica (idraulica). Effetti
della resistenza viscosa sul lancio di un punto materiale.
Diminuzione della gittata. Soluzione esatta ed approssimata. Moto
verticale di un grave nell'aria (caso del paracadute). Esperienza
di Millikan e calcolo della carica elementare. Moto di una
particella carica in presenza di un campo magnetico (cenni). Moto
di una carica elettrica in un campo elettrico ed in un campo
magnetico sovrapposti. Caso di B ed E
fra loro ortogonali.
DINAMICA DEL PUNTO MATERIALE VINCOLATO.
Prima analisi del concetto di vincolo. Definizione di
vincolo semplice, doppio e triplo. Definizione e
caratterizzazione delle velocità possibili. Vincoli mobili.
Velocità virtuali e velocità di trascinamento. Significato ed
esempi di velocità virtuale. Esempio di vincolo semplice e
doppio. Prima definizione di vincolo liscio. Caratterizzazione
dei vincoli lisci (potenza virtuale nulla). Principio dei lavori
virtuali. Considerazioni energetiche. Teorema delle forze vive
per il punto vincolato. Bilancio energetico in un sistema non
inerziale. Equazioni di moto di un punto vincolato ad una linea
(fissa e liscia) o ad una superficie. Equilibrio di un punto
vincolato ad una linea. (Il metodo dei moltiplicatori di
Lagrange).
TEOREMI GENERALI SUI SISTEMI DI PUNTI
MATERIALI.
Classificazione delle forze: forze interne ed esterne,
forze attive e reazioni vincolari. Equazioni cardinali della
dinamica e loro derivazione. Commenti sulle equazioni cardinali
della dinamica. Equazioni cardinali della statica. Caso dei
sistemi rigidi. Sistemi composti da più parti rigide. Questioni
energetiche. Sistemi di forze conservative. Potenziale di sistemi
conservativi di forze interne e di forze esterne.
GEOMETRIA E CINEMATICA DELLE MASSE.
Centro di massa e proprietà. Centro di gravità.
Calcolo del centro di massa di alcune figure piane e solide
(triangolo, arco di circonferenza, settore circolare, semidisco,
tetraedro). Momenti statici. Momenti di secondo grado (rispetto
ad un punto, ad una retta, ad un piano). Momenti centrifughi.
Espressione del momento d'inerzia rispetto ad una retta generica.
Matrice di inerzia. Costruzione dell'ellissoide di inerzia.
Richiami sul teorema spettrale per applicazioni lineari
simmetriche. Assi principali di inerzia e forma canonica
dell'ellissoide d'inerzia. Proprietà geometrico-materiali degli
assi principali di inerzia. Esercizi ed esempi di ricerca della
terna principale. Teorema di Huygens. Dimostrazione nel caso di
momento d'inerzia rispetto ad un punto, una retta ed un piano e
di un momento centrifugo. Determinazione di momenti d'inerzia di
particolari sistemi materiali omogenei (asta, lamina rettagolare,
quadrato, triangolo, parallelepipedo, cubo, circonferenza, disco,
semidisco, superficie sferica, sfera, semisfera, cubo, cilindro,
cono). Proprietà di stazionarietà degli assi principali. Punti
stazionari di una forma quadratica. Ricerca degli assi principali
in una lamina rettangolare. Esempio di diagonalizzazione
dell'omografia di inerzia (per la lamina quadrata). Cinematica
delle masse. Quantità di moto e momento della quantità di moto.
Moto relativo al centro di massa. Teorema del centro di massa.
Energia cinetica. Teorema di Konig. Dimostrazione. Il caso dei
sistemi rigidi. Espressione di Q, T, K tramite la
matrice d'inerzia. Le formule 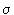 (O)
(O) 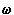 e
e 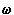
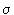 (O)
(O) 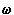 . Calcolo di K e T nel
caso di sistemi rigidi.
. Calcolo di K e T nel
caso di sistemi rigidi.
MECCANICA DEI SISTEMI OLONOMI.
Introduzione alla meccanica dei sistemi. Sistemi
olonomi. Vincoli olonomi: compatibilità ed indipendenza.
Coordinate lagrangiane. Spazio delle configurazioni. Esempi di
spazi delle configurazioni. Velocità possibili. Stato cinematico
di un sistema olonomo. Spazio delle fasi. Spazio tangente allo
spazio delle configurazioni. Velocità virtuali.
Caratterizzazione degli atti di moto virtuale. Spazio normale
allo spazio delle configurazioni. Richiami della dinamica del
punto vincolato ad una linea o ad una superficie. Vincoli olonomi
lisci. Significato geometrico e meccanico del vincolo. Potenza
virtuale delle reazioni. Principio dei lavori virtuali.
Caratterizzazione di vincoli bilateri lisci. Equazioni di
Lagrange di I specie. Forze generalizzate. Statica dei sistemi
olonomi a vincoli lisci. Equazione simbolica della statica.
Statica dei sistemi rigidi. Applicazione del principio dei lavori
virtuali. Equazione simbolica della dinamica dei sistemi.
Equazioni di Lagrange di II specie e loro dimostrazione. Sistemi
di forze conservative e funzione Lagrangiana. Applicazioni del
formalismo lagrangiano: il caso del punto libero nello spazio, il
pendolo composto. Esercizi sulle equazioni di Lagrange e sulla
dinamica dei corpi rigidi.
MECCANICA DEI SISTEMI RIGIDI.
Sistemi rigidi liberi. Precessioni. Equazioni di
Eulero. Precessioni per inerzia. Moto alla Poinsot. Proprietà
dinamiche degli assi principali d'inerzia. Rotazione di un corpo
rigido intorno ad un asse fisso. Stabilità degli assi permanenti
di rotazione. Cenni sugli effetti giroscopici.
COMPLEMENTI.
ANALISI QUALITATIVA DELLE EQUAZIONI DIFFERENZIALI.
Sistema di equazioni differenziali del primo ordine.
Spazio delle configurazioni e spazio delle fasi. Scopi
dell'analisi qualitativa. Sistemi autonomi e non
autonomi. Piano delle fasi. Orbite. Spazio delle fasi e
delle fasi estesi. Campo delle direzioni. Cenno allo
studio del campo delle direzioni e del flusso. Equazioni
del 2° ordine nel piano delle fasi. Soluzione di sistema
lineare del 2° ordine. Sistema di due equazioni
differenziali del 1° ordine. Punti di equilibrio. Punti
di equilibrio stabile e di equilibrio instabile.
Applicazioni. Oscillatore armonico. Soluzione
esatta. Analisi qualitativa dell'oscillatore armonico.
Ricerca della soluzione con l'uso dell'algebra lineare.
Cenno alla stabilità di sistemi lineari. Stabilità e
stabilità asintotica. Studio in funzione degli
autovalori e degli autovettori. Analisi dei vari casi:
nodo stabile instabile, punto sella, centro, fuoco
stabile ed instabile. Pendolo nonlineare. Il problema
matematico. Analisi qualitativa del pendolo nonlineare.
Sistemi conservativi. Stabilità dell'equilibrio tramite
l'analisi dell'energia potenziale.
STABILITÀ DELL'EQUILIBRIO DEI SISTEMI OLONOMI.
Definizione di stabilità e di stabilità asintotica.
Definizione di instabilità . Equilibrio indifferente.
Criteri di stabilità di Liapunov. Criteri di Dirichlet
per la stabilità dell'equilibrio. Ricerca di posizioni
di equilibrio e stabilità.
L PROBLEMA DELLE PICCOLE OSCILLAZIONI. Il problema
delle piccole oscillazioni attorno alla configurazione di
equilibrio stabile. La Lagrangiana per le piccole
oscillazioni. Equazioni di moto per le piccole
oscillazioni per un sistema conservativo a vincoli fissi.
Modi normali di oscillazione. Il problema accoppiato.
Frequenze proprie. Coordinate e oscillazioni normali.
Applicazioni: moto unidimensionale, pendolo doppio,
pendoli accoppiati con una molla, oscillazioni della
molecola triatomica.
MECCANICA DEI SISTEMI CONTINUI. Sistemi
materiali continui: forze di massa e forze di superficie.
Stato di tensione. Teorema di Cauchy. Equazione
indefinita di equilibrio. Simmetria degli sforzi. Caso
dei fluidi: l'equazione della fluidostatica, caso dei
fluidi barotropici, l'energia delle pressioni e
integrazione dell'equazioni di equilibrio. Caso dei gas
perfetti in condizioni isoterme, l'equazione barotropica.
Caso dei liquidi e statica dei liquidi pesanti. Dinamica
dei fluidi perfetti. Punto di vista euleriano e punto di
vista di flusso. Il trinomio di Bernoulli. Il teorema di
Bernoulli sia in generale che nella forma degli
idraulici.
LIBRI di RIFERIMENTO:
G.Frosali, Appunti delle lezioni di Meccanica
Razionale, Dispense distribuite a lezione, 1999
D.Quilghini, Appunti delle lezioni di Meccanica
Razionale, Dattiloscritto, Firenze, 1995 .
A.Fasano, V.de Rienzo, A.Messina, Corso di
Meccanica Razionale, Laterza, Bari, 1989.
G. Borgioli, Modelli Matematici di Evoluzione ed
Equazioni Differenziali, Celid, Torino, 1996
Gli argomenti in corsivo sono facoltativi.
Firenze, 12 giugno 2000
Elenco delle
lezioni tenute dal Prof. Frosali nel corso dell'anno acc. 1999-00
Programma del Corso
dell'anno acc. 1997-98
Programma del Corso
dell'anno acc. 1998-99
Torna all'Home
Page di Giovanni Frosali