


Next: Anal. mat. I -
Up: No Title
Previous: Anal. mat. I -
ES.1
L'affermazione: Sia
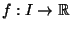 derivabile, allora f é
decrescente se e solo se f'< 0 su I é
vera o falsa?
derivabile, allora f é
decrescente se e solo se f'< 0 su I é
vera o falsa?
ES.2
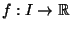 si dice Lipschitziana in I se esiste k>0 tale che
si dice Lipschitziana in I se esiste k>0 tale che
Dimostrare che se
![$f:[a,b]\rightarrow\R$](img78.gif) è C1, allora è
Lipschitziana (usare il teorema di Lagrange).
è C1, allora è
Lipschitziana (usare il teorema di Lagrange).
Verificare che il valore assoluto è Lipschitziana in [-7,7].
ES.3
Verificare che la funzione
![$f:[-1,3]\rightarrow \R\ x\mapsto (x^2+1)^{(x+2)}$](img79.gif) è invertibile e determinare
D4f-1(0).
è invertibile e determinare
D4f-1(0).
I seguenti esercizi sono parte di prove di esame
per l'Anno Accademico 97/98
ES.4
Determinare il massimo k per cui 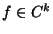 in un intorno di 0
in un intorno di 0
ES.5 Sapendo che
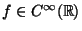 e che
e che
a) Determinare
f(3)(0),
b) Quante derivate di (f(x))2 in x=0 posso determinare?
c) Esprimere in forma di Lagrange
f(1)-1-1/3
ES.6 Sapendo che
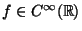 e che
e che
a) Determinare
f(4)(1)
b) Determinare
f(5)(1)
c) Quante derivate in x=1 posso determinare?
d) Esprimere in forma di Lagrange
ES.7
a) Determinare il polinomio di Taylor di grado 4 in 0della funzione
f(x)=ex+2x2-x-5x2/4
b) Posso decidere se f(0) e' massimo o minimo relativo per la
funzione usando la risposta al punto a)? In caso affermativo indicare
cosa sia.
ES.8)
a) Determinare il polinomio di Taylor di grado 4 in 0della funzione
b) Posso decidere se f(0) e' massimo o minimo relativo per la
funzione usando la risposta al punto a)? In caso affermativo indicare
cosa sia.
ES.9) Calcolare al variare di
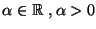



Next: Anal. mat. I -
Up: No Title
Previous: Anal. mat. I -
Gianna Stefani
1998-11-27