


Next: About this document ...
Up: No Title
Previous: Anal. mat. I -
I seguenti esercizi sono stati proposti il 17/11/97
2) Determinare numero e segno delle soluzioni della seguente equazione
(4x3+7x2-6x+7) lg(x+1/2)=0
3) Studiare e disegnare il grafico in [0,1] della funzione
4) Data la funzione
i) verificare che e' continua su tutto R e determinare dove e' positiva,
negativa o nulla
ii) calcolare i limiti per
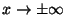
iii) dedurre che la funzione ammette max e min assoluti e calcolarli
iv) disegnare il grafico
5) Sia
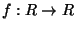 derivabile e tale che
derivabile e tale che
Provare che
6) Trovare l'insieme dei
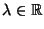 per i quali la seguente equazione ha
almeno una soluzione positiva
per i quali la seguente equazione ha
almeno una soluzione positiva
7) Calcolare
f(5)(-1), se
Si consiglia di calcolare il polinomio di Taylor usando come nuova
variabile l'incremento rispetto a -1.
8) Studiare la convergenza delle seguenti successioni
9) Studiare al variare di
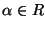 la convergenza delle successioni
la convergenza delle successioni



Next: About this document ...
Up: No Title
Previous: Anal. mat. I -
Gianna Stefani
1998-11-27
![\begin{displaymath}\sqrt[3]{\frac{(x-1)^2}{1+(x-1)^4}}\end{displaymath}](img90.gif)