


Next: Anal. mat. I -
Up: No Title
Previous: Anal. mat. I -
ES.1
Determinare l'immagine delle funzioni che compaiono nei
precedenti esercizi.
ES.2
Determinare estremo superiore, estremo inferiore ed gli eventuali massimi e
minimi relativi e assoluti delle funzioni che compaiono nei
precedenti esercizi.
ES.3 Determinare l'insieme in cui le seguenti funzioni
sono derivabili e calcolare la derivata. Calcolare inoltre
le eventuali derivate destre e sinistre ed gli eventuali punti a
tangente verticale, tutte le funzioni devono intendersi estese per continuita'
ove e' possibile.
ES.4
Sia
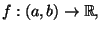 continua e derivabile,
dimostrare che se
continua e derivabile,
dimostrare che se
allora f ha un punto con derivata zero.
ES.5
Sia
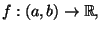 una funzione crescente (decrescente)e
derivabile, posso affermare che la sua derivata non si annulla?.
una funzione crescente (decrescente)e
derivabile, posso affermare che la sua derivata non si annulla?.
I seguenti esercizi sono parte di prove di esame
per l'Anno Accademico 97/98
ES.6 Continuazione dell'Es.9 del 6/11/98
c) Determinare gli eventuali punti di max e min relativo e assoluto
d) Disegnare il grafico della funzione
e) Giustificare l'affermazione :
f|[-1 ,1]ha massimo e
minimo assoluti e calcolarli
g) Determinare al variare di 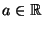 il numero ed il segno
delle soluzioni di
il numero ed il segno
delle soluzioni di
f(x)=a
h) Facoltativo. Disegnare sul retro il grafico della funzione
g(x)=f(x) - [f(x)],
si ricordi che [y] e' la parte intera di y.
ES.7
a) Giustificare l'affermazione: f ha massimo e minimo in [1,3]e calcolarli
b) Disegnare il grafico della funzione e determinarne l'immagine e gli
eventuali punti di massimo e minimo relativo e assoluto
ES.8
Determinare al variare di 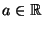 numero e segno delle radici reali del seguente
polinomio.
numero e segno delle radici reali del seguente
polinomio.
ES.9
Determinare al variare di 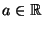 numero e segno delle radici reali del seguente
polinomio.
numero e segno delle radici reali del seguente
polinomio.



Next: Anal. mat. I -
Up: No Title
Previous: Anal. mat. I -
Gianna Stefani
1998-11-27