


Next: Anal. mat. I -
Up: No Title
Previous: Anal. mat. I -
ES.1 Determinare gli eventuali limiti delle seguenti successioni
ES.2
Determinare per quali delle funzioni che compaiono nei
precedenti esercizi posso decidedere se l'immagine è un intervallo
limitato o illimitato in base al calcolo dei limiti e
alle proprietà delle funzioni continue su intervalli.
ES.3
Determinare per quali delle funzioni che compaiono nei
precedenti esercizi posso decidedere sull'esistenza di massimo e
minimo in base al calcolo dei limiti e
alle proprietà delle funzioni continue su intervalli.
ES.4
Sia
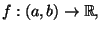 continua
dimostrare che se
continua
dimostrare che se
allora f ha minimo e non ha massimo. (Suggerimento:
aiutarsi con l'intuizione per capire come la definizione di limite
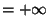 permetta di restringere la funzione ad un sottointervallo
chiuso e applicare il teorema di Weierstrass).
permetta di restringere la funzione ad un sottointervallo
chiuso e applicare il teorema di Weierstrass).
ES.5
Sia
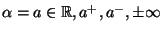 punto di accumulazione per
punto di accumulazione per 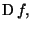 dimostrare che se
dimostrare che se
allora f e' inferiormente illimitata.
ES.6
Sia
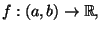 una funzione monotona.
Dimostrare che se f e' discontinua in
una funzione monotona.
Dimostrare che se f e' discontinua in
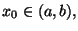 allora f(x0) e' l'unico punto dell'intervallo di estremi
allora f(x0) e' l'unico punto dell'intervallo di estremi
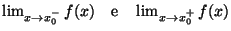 che appartiene all'immagine di f.
che appartiene all'immagine di f.
ES.7
Sia
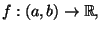 una funzione crescente (decrescente)
la cui immagine
e'
una funzione crescente (decrescente)
la cui immagine
e'
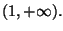 Calcolare
Calcolare
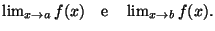 Dimostrare che la funzione e' continua (usare il precedente esercizio).
Dimostrare che la funzione e' continua (usare il precedente esercizio).
ES.8 Provare che non esiste una funzione continua
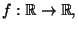 tale che
tale che
e trovarne una tale che
ES.8 Per quali valori di
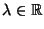 le seguenti funzioni
ammettono asintoti obliqui?
le seguenti funzioni
ammettono asintoti obliqui?
I seguenti esercizi sono parte di prove di esame
per l'Anno Accademico 97/98
ES.9
a) Determinare il dominio di f e
le equazioni degli eventuali asintoti
b) Giustificare l'affermazione :
f|[-1 ,1]ha massimo e minimo assoluti
......
ES.10 Dare la definizione di
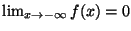 e verificare, usando la definizione, che
e verificare, usando la definizione, che



Next: Anal. mat. I -
Up: No Title
Previous: Anal. mat. I -
Gianna Stefani
1998-11-27