Anal. mat. I - Esercizi del 30/10/98

ES.1 Determinare per quali delle funzioni che compaiono nei precedenti esercizi ha senso porsi il problema di calcolare il limite per $x\rightarrow \pm\infty.$
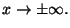
ES.2 Determinare gli eventuali asintoti orizzontali, verticali e obliqui per le funzioni che compaiono nei precedenti esercizi.
I seguenti esercizi sono parte di prove di esame per l'Anno Accademico 97/98
ES.3

$$\mbox{Definiamo} \hspace*{5cm} f:x\mapsto 1/ \sqrt{\vert\sin\,x\vert}\ .\hspace*{5cm}$$

a) Determinare il dominio di f
b) Determinare le equazioni degli eventuali asintoti
f) Determinare massimo e minimo di $f_{\vert[\frac{\pi}{4} ,\frac{5\pi}{6}]}$
ES.4

$$\mbox{Definiamo} \hspace*{5cm} f:x\mapsto \arctan\left(\frac{ \vert x\vert+5}{x+5}\right) .\hspace*{5cm}$$

a) Determinare il dominio di f
b) Determinare le equazioni degli eventuali asintoti
c) Determinare gli eventuali punti di discontinuita' e classificarli
ES.5

$$\mbox{Definiamo} \hspace*{5cm} f:x\mapsto \sqrt{1-x^2+x} .\hspace*{5cm}$$

a) Calcolare il massimo e minimo globale di f.
ES.6

$$\mbox {Sia} \hspace*{5cm} f:x\mapsto e^{(x-1)\,\log\,\vert x+2\vert} \hspace*{5cm}$$

a) Determinare il dominio ed eventuali asintoti verticali orizzontali e obliqui
b) Giustificare l'affermazione: f ha massimo e minimo assoluti in [2,3] (usare le proprietà delle funzioni elementari) e calcolarli.
c) Facoltativo Verificare che f e' crescente in $(-\infty,-3]$
ES.7 Sia

$$f: x\mapsto \frac{ \vert x\vert\sin\,x}{1-\cos\,x},\quad x\in (-\pi,2\pi).$$

a) Determinare il dominio di f
b) Determinare le equazioni degli eventuali asintoti
ES.8

$$\mbox{Definiamo} \hspace*{5cm} x\mapsto \arctan\left(\frac{ 7+x}{7-\vert x\vert}\right) .\hspace*{5cm}$$

a) Determinare il dominio di f
b) Determinare le equazioni degli eventuali asintoti
c) Determinare gli eventuali punti di discontinuita' e classificarli
ES.9 Sia

$$x\mapsto \frac{\vert x\vert}{\sin\,x\sqrt{\cos\,x}}, \quad x\in (-\pi/2,\pi/2).$$

a) Determinare il dominio di f
b) Determinare le equazioni degli eventuali asintoti
c) Determinare gli eventuali punti di discontinuita' e classificarli