Next: Anal. mat. I -
Up: No Title
Previous: Anal. mat. I -
ES.1 Determinare quali delle funzioni che compaiono negli esercizi
del 10/10/98 sono invertibili e calcolare le eventuali inverse e il loro dominio.
Stesso esercizio considerando le restrizioni delle precedenti funzioni alla
semiretta
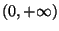
ES.2 Sia
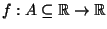 limitata e
limitata e
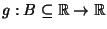 tale che
tale che
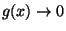 per
per
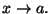 Supponendo che a sia di accumulazione per
Supponendo che a sia di accumulazione per 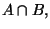 dimostrare che
dimostrare che
ES.3 Dimostrare che
ES.4 Delle funzioni che compaiono negli esercizi
del 10/10/98 e delle seguenti funzioni determinare il dominio e l'insieme
dove sono continue. Determinare inoltre gli eventuali asintoti verticali e quali
di esse siano estendibili per continuita'. Classificare inoltre le
eventuali discontinuita'.
ES.5 Determinare per quali valori dei parametri le seguenti
funzioni sono continue
ES.6 i) Determinare i valori 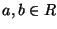 che rendono continua su
tutto R la funzione
che rendono continua su
tutto R la funzione
Per la funzione determinata al punto i) :
ii) determinare eventuali asintoti verticali e gli intervalli
di crescenza o decrescenza
(usare le proprieta' delle funzioni elementari)
iii) disegnare il grafico e determinare, se esistono, massimo e minimo
iv) la f e' invertibile? Lo e' qualche sua restrizione? In caso
affermativo determinare l'inversa.
ES.7 Usando la definizione, verificare che
ES.8 Dimostrare che se
allora
Quanto vale



Next: Anal. mat. I -
Up: No Title
Previous: Anal. mat. I -
Gianna Stefani
1998-11-27
![\begin{displaymath}x\mapsto \begin{cases}
\frac{\sin(x)}{\sqrt[3]x}\quad&\text{s...
...ext{se}\quad x\not= 0\cr
-3\quad&\text{se}\quad x=0
\end{cases}\end{displaymath}](img31.gif)
![\begin{displaymath}x\mapsto \begin{cases}
\frac{a+\cos(x)}{\sqrt[3]x}\quad&\text...
...quad x\in [1,2] \cr
3-x\quad&\text{se}\quad x>2 \cr
\end{cases}\end{displaymath}](img32.gif)