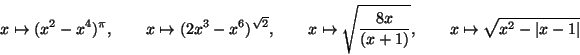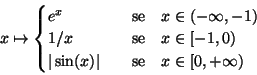Anal. mat. I - Esercizi del 10/10/98

ES.1 Determinare il dominio, l'immagine, gli estremi inferiore e superiore e, se esistono, il massimo e minimo globale delle seguenti funzioni. Determinare inoltre quali di esse siano pari dispari o periodiche. Infine cercare di discutere la loro monotonia.

$$x\mapsto \frac{ e^{(x^2)}-1}{ e^{(x^2)}+1},\quad\quad x\mapst... ...\quad\quad x\mapsto \frac{ \arctan\,x+\pi/2}{ \arctan\,x-\pi/2}$$

$$x\mapsto (x^2-x^4)^\pi,\quad\quad x\mapsto (2x^3-x^6)^{\sqrt ... ...\frac{8x}{(x+1)}},\quad\quad x\mapsto \sqrt{x^2-\vert x-1\vert}$$

$$x\mapsto \frac{\vert x+1\vert}{1-x},\quad\quad x\mapsto log_... ... \arcsin\sqrt{1/2-x^2},\quad\quad x\mapsto \tan(\vert x+1\vert)$$

$$x\mapsto \log(\sin(\vert x\vert)),\quad\quad x\mapsto \arcsin... ...mapsto e^{\arctan(x+1)},\quad\quad x\mapsto \sqrt{\arccos(x)-1}$$

 
ES.2 Disegnare il grafico delle funzioni

$$x\mapsto \max\{ \vert x\vert, 1/x\},\quad\quad x\mapsto (e^x-... ... x\mapsto \vert x^3-1\vert,\quad\quad x\mapsto \vert x\vert^3-1$$

$$x\mapsto x-[x],\quad\quad x\mapsto \sin(x)-[\sin(x)],\quad\quad x\mapsto [\log(x)],\quad\quad x\mapsto (\log(x))^-$$

 
ES.3 Siano date

$$f:x\mapsto \frac{x+1}{4x},\quad\quad g:x\mapsto x^2-1$$

determinare 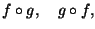$f\circ g,\quad g\circ f,$ il loro dominio e la loro immagine.
 
ES.4 Disegnare il grafico delle funzioni

$$x\mapsto \sin(x+1),\quad\quad x\mapsto \sin(x)+1 ,\quad\quad x\mapsto (0.5)^{x+1},\quad\quad x\mapsto \log\vert x+1\vert$$

$$x\mapsto \begin{cases} e^x\quad&\text{se}\quad x\in (-\infty,... ...rt\sin(x)\vert\quad&\text{se}\quad x\in [0,+\infty) \end{cases}$$

$$x\mapsto \cos(2x),\quad\quad x\mapsto -3\cos(x)+1 ,\quad\quad x\mapsto \tan(x+1),\quad\quad x\mapsto cotan (3x)$$

 
ES.5 Determinare quali delle funzioni dell'esercizio 2 sono crescenti, decrescenti, pari, dispari o periodiche. Nel caso di funzioni peiodiche determinare il periodo minimo.
 
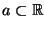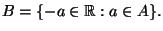ES.6 Sia $a\subset \R$ e sia $B=\{-a\in\R : a\in A \}.$ Dimostrare che

$$\sup\,A=y\in \R\quad\Longrightarrow\quad \inf\,B=-y.$$

 
ES.7 Determinare l'immagine, gli estremi inferiore e superiore e, se esistono, il massimo e minimo globale delle seguenti funzioni (successioni) $f : \N \subseteq \R \rightarrow \R$

$$n\mapsto \frac{7-n}{n},\quad\quad n\mapsto \frac{2+n}{n+1} ,\quad\quad n\mapsto \frac{1+n^2}{n}$$

 
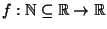
ES.8 Per ogni 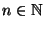$n\in \N$ definiamo

$$I_n=\quad\quad [0,(1+n)/(n)],\quad\quad (1-1/n,1),\quad\quad [1,1+1/n] ,\quad\quad (-1/n,1/n)$$

Determinare

$$\bigcap_{n\in\N}I_n$$