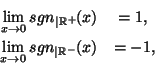
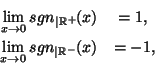
Se
Ad esempio la funzione sgn non è continua nè a destra nè a sinistra, mentre la funzione parte intera è continua a destra.
Dopo una semplice riflessione sulle definizioni di limite e limite destro e sinistro
possiamo affermare che
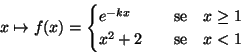
Inoltre, per la continuità della funzione esponenziale, otteniamo