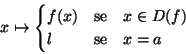Esempio 5
Verifichiamo con la definizione che, come il grafico suggerisce,
Poichè se
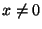
si ha
fissato
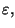
ottengo che
ed il limite è verificato.
Esempio 6
Osserviamo il Grafico disegnato per punti della funzione
Il grafico di questa funzione è rappresentato da una linea molto
liscia e, anche se la formula non definisce
un numero per
x=0,siamo portati a dire che siamo in presenza di una funzione continua che ha valore
1 per
x=0, questa idea intuitiva è resa precisa dalla verifica del limite.
Se verifichiamo che
possiamo considerare il dominio della funzione tutto l'asse
reale ed il suo valore in 0 uguale ad 1.
Per la verifica è necessaria la disuguaglianza
che si ottiene con cosiderazioni di geometria elementare.
Da questa disuguaglianza dividendo per
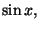
considerando i reciproci e
tenendo conto che
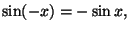
si ottiene
da cui
Se scegliamo un qualsiasi numero reale
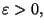
possiamo definire
e la precedente disuguaglianza
ci dice che
La definizione di limite è quindi verificata.