Definizione 3.1
Consideriamo una funzione
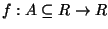
e sia
a un punto di accumulazione per
A.
Diremo che
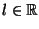
è il
limite di
f(
x)per
x che tende a
a, e scriveremo
se per ogni
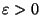
esiste un
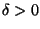
tale che:
o equivalentemente in termini di intorni
Una scrittura equivalente è
che si legge:
f(
x) tende
ad
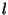
per
x che tende ad
a.