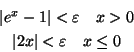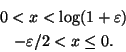Esempio 4
Studiamo la continuità della funzione definita da
Il Lemma precedente ci dice che la funzione è continua in
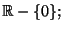
infatti, se
a>0esiste un intorno
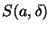
su cui
f coincide con la funzione
esponenziale che è continua, se
a<0 esiste un intorno
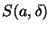
su cui
f coincide con un polinomio che sappiamo essere
continuo.
Resta solo da analizzare la continuità in a=0.Poichè f(0)=1, per verificare la continuità in
0, considero
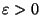 e studio le disequazioni
e studio le disequazioni
che hanno come soluzione rispettivamente
Si osserva che
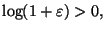
quindi possiamo
scegliere
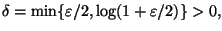
ottenendo la
continuità della funzione in 0 e quindi su tutto
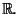
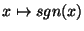 che è discontinua in 0
che è discontinua in 0
![$x\mapsto [x]$](img48.gif) che è discontinua in ogni
che è discontinua in ogni 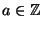
![]() è continua in a.
è continua in a.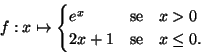
![]() e studio le disequazioni
e studio le disequazioni