


Next: Classi di funzioni continue
Up: No Title
Previous: No Title
Intuitivamente, diciamo
che una funzione f è continua in un punto a
se l'errore
|f(x)-f(a)| che commetto nel considerare f(x)uguale al suo valore in a può essere reso arbitrariamente
piccolo purchè la variabile x sia sufficientemente vicina ad
a. Le parole arbitrariamente piccolo e sufficientemente vicino sono
vaghe e dovranno essere quantificate con una definizione precisa.
Definizione 1.1
Sia
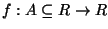
e sia
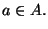
Mentre l'idea intuitiva di continuità sembra ovvia, la sua precisa formulazione
analitica può sembrare inizialmente difficile da comprendere a chi non è abituato
all'uso dei quantificatori. Tuttavia è indispensabile avere un preciso
significato per la parola continuità ed il lettore imparerà ad apprezzare la precisione
logica del linguaggio matematico.
Per aiutare la comprensione della definizione analitica con l'intuizione,
si noti che la traduzione matematica di errore arbitrariamente
piccolo è ottenuta mediante il quantificatore ogni, che
rende arbitraria la scelta dell'errore
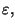 mentre il
quantificatore esiste traduce il sufficientemente vicino e
indica che l'ampiezza
mentre il
quantificatore esiste traduce il sufficientemente vicino e
indica che l'ampiezza 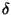 dell'intorno su cui vale l'approssimazione, deve essere scelta in
dipendenza da
dell'intorno su cui vale l'approssimazione, deve essere scelta in
dipendenza da
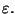
Come facile verifica della definizione di continuità osserviamo
che una funzione costante
è continua in ogni
punto 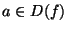 .
Infatti l'errore
|f(x)-f(a)| è sempre 0,quindi qualunque sia
.
Infatti l'errore
|f(x)-f(a)| è sempre 0,quindi qualunque sia
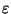 possiamo scegliere
sempre lo stesso
possiamo scegliere
sempre lo stesso 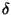 ad esempio
ad esempio 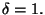
Un secondo semplice esempio è dato dalla funzione identità
che è continua in ogni punto 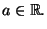 In questo
caso, dato
In questo
caso, dato
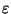 si può scegliere
si può scegliere
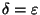 (ma anche
(ma anche
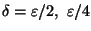 ed ogni altro
ed ogni altro
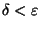 ).
).
Il prossimo esempio è più complicato, ma è anche indicativo del metodo
da usare per verificare la continuità mediante la definizione.
Esempio 1
Vogliamo verificare che la funzione
è continua in
a=0, dove vale 1.
Per prima cosa fissiamo
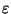
e
consideriamo la disequazione
In generale non
è necessario risolvere la disequazione (cioè trovarne tutte le
soluzioni), ma è sufficiente verificare che fra le soluzioni ci
sono i punti di un intorno di
a. Nel nostro caso la
disequazione diventa
La disequazione può essere
lunga da risolvere, ma a noi interessa che sia verificata in
un intorno di 0 e per questo è sufficiente osservare che
quindi
Abbiamo così verificato che per ogni
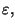
esiste
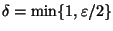
che verifica la condizione
di continuità.
Nell'esempio precedente abbiamo usato la definizione per
verificare la continuità in un punto interno al dominio, ma è
facile anche vedere che una funzione f è continua in ogni
punto 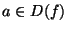 che sia isolato.
La definizione in questo caso appare inutile, ma viene data in
generale per tener conto delle situazioni che possono capitare
combinando fra loro le funzioni elementari, ad esempio la
funzione
che sia isolato.
La definizione in questo caso appare inutile, ma viene data in
generale per tener conto delle situazioni che possono capitare
combinando fra loro le funzioni elementari, ad esempio la
funzione
ha come campo di
esistenza l'insieme
quindi è continua
nel suo insieme di definizione. Si noti che la funzione
è la restrizione della funzione nulla all'insieme A.
Finora abbiamo verificato la continuità di alcune funzioni,
ci sembra utile fare anche alcune verifiche di discontinuità. Poichè
la discontinuità è definita come mancanza di continuità, la sua verifica
sarà un utile esercizio di negazione di una proposizione, cioè come
si può affermare che una proposizione è falsa.
Esempio 2
Come primo esempio intuitivo di funzione discontinua in
a=0,abbiamo considerato la funzione segno, per dare una dimostrazione rigorosa di questo
fatto dobbiamo trovare un numero
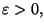
tale che la disequazione
non abbia fra le sue soluzioni un intorno di 0. Poichè la funzione
salta
dal valore 0 ai valori
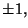
possiamo scegliere
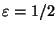
e verificare facilmente
che la disequazione
|
sgn(
x)|<1/2 ha come unica soluzione
x=0, che non contiene
nessun intorno di 0.
Nell'esempio precedente, abbiamo trovato un
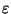 tale che la
corrispondente disequazione ha come soluzione l'unico punto x=0, ma per negare
la continuità è sufficente negare l'esistenza di un intorno di soluzioni,
qual è una formulazione diretta della definizione
di discontinuità?
tale che la
corrispondente disequazione ha come soluzione l'unico punto x=0, ma per negare
la continuità è sufficente negare l'esistenza di un intorno di soluzioni,
qual è una formulazione diretta della definizione
di discontinuità?
L'esempio seguente mostra una funzione che è discontinua in ogni punto del
dominio.
Esempio 3
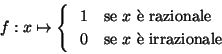
La
funzione di Dirichlet definita da
è discontinua in ogni
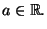
La discontinuità dipende dal fatto che in ogni intervallo ci sono
sia numeri razionali che numeri irrazionali. Dimostriamo che
la precedente funzione è discontinua in un punto razionale, si consiglia di
ripetere la dimostrazione nel caso di un punto irrazionale.
Per affermare che la funzione di Dirichlet è discontinua in 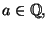 si
deve trovare un
si
deve trovare un
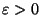 tale che per ogni
tale che per ogni 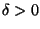 esiste
esiste
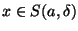 con la proprietà
con la proprietà
Nel nostro caso se scegliamo
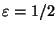
tutti i punti irrazionali
xsoddisfano
Basterà quindi scegliere
un numero irrazionale
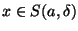
per ottenere la discontinuità della
funzione in
a.
Concludiamo il capitolo descrivendo la più importante conseguenza
della continuità in un punto. Questa proprietà va sotto il nome di
permanenza del segno
ed afferma che se una funzione è diversa da zero in un punto di continuità
conserva lo stesso segno per punti vicini.
Teorema 1.1 (Permanenza del segno)
Se
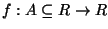
è continua in
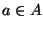
e
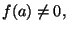
allora esiste un intorno
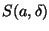
tale che
o equivalentemente



Next: Classi di funzioni continue
Up: No Title
Previous: No Title
Gianna Stefani
1998-12-03
![]() mentre il
quantificatore esiste traduce il sufficientemente vicino e
indica che l'ampiezza
mentre il
quantificatore esiste traduce il sufficientemente vicino e
indica che l'ampiezza ![]() dell'intorno su cui vale l'approssimazione, deve essere scelta in
dipendenza da
dell'intorno su cui vale l'approssimazione, deve essere scelta in
dipendenza da
![]()
![]() si
deve trovare un
si
deve trovare un
![]() tale che per ogni
tale che per ogni ![]() esiste
esiste
![]() con la proprietà
con la proprietà