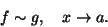Next: Formula di Taylor
Up: No Title
Previous: Differenziale
Poniamoci il problema di cercare approssimazioni polinomiali sempre migliori
di una funzione. Per far questo dobbiamo prima di tutto definire cosa intendiamo
per "approssimazioni migliori". Questo concetto è espresso dalla definizione di
funzione infinitesima e del suo ordine.
Le funzioni considerate in questo capitolo si suppongono tutte definite
sullo stesso intervallo I.
Definizione 11.1
-
Diremo che f è infinitesima per
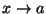 e scriveremo
e scriveremo
se
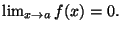
-
Diremo che f è un infinitesimo di ordine superione a g per
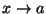 e scriveremo
e scriveremo
se f e g sono due funzioni infinitesime e
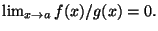
-
Diremo che f è un infinitesimo dello stesso ordine di g per
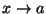 se la funzione f/g è limitata in un intorno di a, e scriveremo
se la funzione f/g è limitata in un intorno di a, e scriveremo
-
Diremo che f è un infinitesimo equivalente (oppure asintotico) a g per
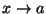 se
se
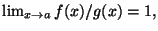 in questo caso scriveremo
in questo caso scriveremo
Definizione 11.2
-
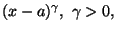 si dice infinitesimo
principale per
si dice infinitesimo
principale per
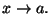
-
Diremo che f è un infinitesimo di ordine superiore a
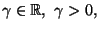 per
per
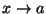 se
se
-
Diremo che f è un infinitesimo di ordine
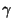 per
per
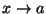 se
se
-
Diremo che
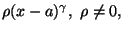 è la parte principale di f per
è la parte principale di f per
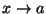 se
se
Nota 4
-
Quanto detto in precedenza può essere esteso al caso
-
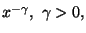 si dice infinitesimo
principale per
si dice infinitesimo
principale per
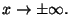
Quando sia chiaro dal contesto quale sia il punto a nell'intorno del quale
stiamo lavorando, eviteremo di scrivere ogni volta
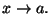
Con gli infinitesimi si possono fare calcoli algebrici che sono una conseguenza diretta
della loro definizione (vedi libro).



Next: Formula di Taylor
Up: No Title
Previous: Differenziale
Gianna Stefani
1998-12-03
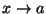 e scriveremo
e scriveremo
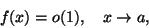
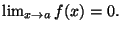
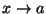 e scriveremo
e scriveremo
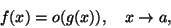
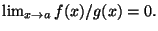
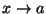 se la funzione f/g è limitata in un intorno di a, e scriveremo
se la funzione f/g è limitata in un intorno di a, e scriveremo
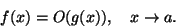
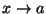 se
se
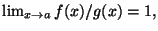 in questo caso scriveremo
in questo caso scriveremo