Next: About this document ...
Up: No Title
Previous: Infinitesimi
Il paragrafo precedente ci permette di chiarire meglio cosa intendiamo
per "approssimazione migliore", infatti diremo che un polinomio approssima meglio
di un'altro una funzione se l'errore che commettiamo nel primo caso è un infinitesimo
di ordine superiore a quello che commettiamo nel secondo caso. Per essere più
precisi, lo scopo di questo paragrafo è di determinare opportune ipotesi per
la funzione
affinché si possa determinare, per ogni 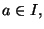 un polinomio di grado
un polinomio di grado
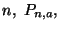 con la proprietà che l'errore (o resto)
con la proprietà che l'errore (o resto)
Rn,a=f-Pn,a
che commettiamo nel
sostituire il polinomio alla funzione sia un infinitesimo di ordine superiore a n, cioè
Contestualmente ci porremo il problema fondamentale di dare una stima
del resto.
Abbiamo già visto i casi n=0,1. Infatti se una funzione è continua, allora è
approssimabile con una costante (polinomio di grado zero), se la funzione è derivabile
allora è approssimabile, nel senso precedentemente detto, con un polinomio lineare.
Per fare un passo avanti nella determinazione dell'approssimazione polinomiale di
una funzione, assumiamo che la funzione sia derivabile due volte in I e fissiamo
il punto a nel quale vogliamo fare l'approssimazione. Per semplicità di scrittura
tralasciamo l'indice a sia nel polinomio approssimante che nel resto,
ottenendo
R1(x)=f(x)-f(a)-f'(a)(x-a)=f(x)-P1(x).
Abbiamo così che il resto è derivabile due volte e vogliamo confrontarlo
con la funzione (x-a)2.
Proposizione 12.1
Se
f è derivabile due volte in
I, allora
- 1.
-
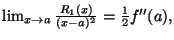
- 2.
- per ogni
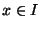 (per semplicità di scrittura
supponiamo x>a) esiste
(per semplicità di scrittura
supponiamo x>a) esiste
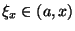 (dipendente da x) tale che
(dipendente da x) tale che
Dimostrazione 12.1
Dalla definizione del resto segue immediatamente che
- 1.
- La dimostrazione si fa applicando il Teorema di Cauchy (vedi libro), che
nel nostro caso si riduce ad applicare il teorema di Rolle alla funzione della
variabile t
Si noti che nella precedente funzione x va considerato costante e si verifichi
che 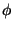 soddisfa alle ipotesi del teorema di
Rolle in [a,x].
soddisfa alle ipotesi del teorema di
Rolle in [a,x].
Otteniamo che esiste
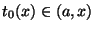 tale che
tale che
Passando al limite per
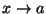 otteniamo l'asserto.
otteniamo l'asserto.
- 2.
- Per il secondo punto si applica ancora il Teorema di Rolle alla funzione
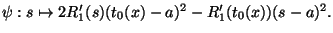
Nota 5
-
Per ottenere il precedente punto 1. basta l'esistenza di
f' su I e quella di f''(a).
-
Se
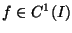 il punto 1. si ottiene dal punto 2.
il punto 1. si ottiene dal punto 2.
In generale se f è derivabile n volte, possimo scrivere, per ogni 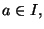 il polinomio di Taylor di f di grado n centrato in a
il polinomio di Taylor di f di grado n centrato in a
Teorema 12.2
Sia
f derivabile
n volte in
I, allora
-
Rn,a=f-Pn,aè un infinitesimo di ordine superiore a n, cioè
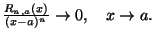 Potremo quindi scrivere
Potremo quindi scrivere
f(x)=Pn,a(x)+o((x-a)n)
che viene chiamata anche formula o approssimazione di Taylor
di ordine n, centrata in a, con resto in forma di Peano.
-
per ogni
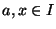 (per semplicità di scrittura
supponiamo x>a) esiste
(per semplicità di scrittura
supponiamo x>a) esiste
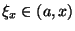 (dipendente da x) tale che
(dipendente da x) tale che
Potremo quindi dire che esiste
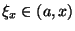 tale che
tale che
che viene chiamata anche formula o approssimazione di Taylor
di ordine n-1, centrata in a, con resto in forma di Lagrange.
-
Se
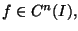 allora
allora
Nota 6
Se
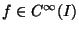
allora possiede approssimazioni di Taylor centrate in ogni
punto di qualsiasi ordine.



Next: About this document ...
Up: No Title
Previous: Infinitesimi
Gianna Stefani
1998-12-03