Differenziale

In questo paragrafo supporremo che

$$f : I \subseteq R \rightarrow R$$

sia derivabile in I.

Definizione 10.1   Chiameremo differenziale di f in a la funzione lineare

$$df_a:\R\rightarrow\R ,\quad h\mapsto f'(a)h$$

Il differenziale in a rappresenta l'approssimazione lineare, nel punto a, dell'incremento dei valori della funzione in dipendenza dell'incremento della variabile.

Se facciamo variare il punto a in I otterremo una funzione di due variabili

$$df:I\times \R\rightarrow \R,\quad (x,h)\mapsto f'(x)h,$$

che viene detta il differenziale di f.

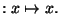
Esempio 9   Calcoliamo il differenziale della funzione identità $:x\mapsto x.$Poiché la sua derivata è identicamente uguale ad 1, ne segue che il suo differenziale è in ogni punto la funzione identità, cioè

$$dx:(x,h)\mapsto h.$$

Va notato che in questa scrittura c'è un po' di ambiguità fra funzione e formula, ma il significato risulta chiaro dal contesto ed inoltre è ormai universalmente accettata questa convenzione.

Usando la precedente notazione per il differenziale della funzione identità, scriveremo

$$df_a=f'(a)dx,\quad df=f'dx,$$

con questa notazione abbiamo espresso il differenziale, che è una funzione di due variabili, come il prodotto di due funzioni di una variabile: la funzione f' che si applica al punto e la funzione dx che si applica all'incremento.