Teorema dei valori intermedi

Teorema 9.1 (dei valori intermedi)   Se f é continua sull'intervallo [a,b] e L é un numero compreso fra f(a) e f(b), allora esiste $c\in [a,b]$ tale che f(c)=L.

Dimostrazione 9.1   Supponiamo che f(a)>L>f(b), lo studente consideri il caso f(a)<L<f(b).

Faremo la dimostrazione nel caso che sia L=0, perché il caso generale si riporta a questo considerando la funzione

$$x\mapsto f(x)-L.$$

Dimostriamo quindi il seguente risultato detto Teorema degli zeri

Sia $f:[a,b]\rightarrow \R$ continua e sia $f(a)>0,\ f(b)<0,$
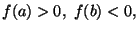
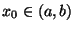
allora esiste $x_0\in (a,b)$ tale che f(x₀)=0.

Il procedimento é basato sulla seguente procedura di iterazione che permette di costruire, a partire da un intervallo che soddisfi le ipotesi del teorema, un sottointervallo di lunghezza metá che soddisfa ancora alle ipotesi del teorema.
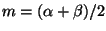
Iterazione. Sia $I=[\alpha,\beta]$ un intervallo che soddisfa alle ipotesi del teorema e sia $m=(\alpha+\beta)/2$ il suo punto medio, scegliamo un nuovo intervallo J in base al valore di f(m)

$$\begin{array}{lll} \text{se} &f(m)=0 &\text{abbiamo trovato l... ...ext{se} &f(m)<0 &\text{si pone} \quad J=[\alpha,m]. \end{array}$$

La procedura di iterazione ci permette di generare una successione decrescente di intervalli nel modo seguente.

• Partiamo dall'intervallo I=[a,b] e generiamo un nuovo intervallo I₁=[a₁,b₁] secondo la procedura di iterazione.
• Se non abbiamo trovato la soluzione, ripetiamo la procedura per trovare I₂=[a₂, b₂] a partire da I₁.
• Procedendo in maniera analoga, se l'algoritmo di bisezione non si arresta, costruiamo una successione decrescente di intervalli

$$I_1\supset I_2\supset\cdots I_n\supset\cdots$$

di lunghezza data da

|b_n-a_n|=|b-a|/2ⁿ.

La completezza dei numeri reali implica che esiste almeno un numero reale x₀appartenente a tutti gli intervalli I_n, il fatto che

$$\inf \{ \vert b_n-a_n\vert,\quad n\in \N \}=0$$

ci dice che tale numero é unico.

Individuato x₀ come candidato, dobbiamo dimostrare che é effettivamente una soluzione dell'equazione. In questo interviene in maniera essenziale l'ipotesi di continuitá attraverso il teorema della permanenza del segno. Infatti, per la procedura che abbiamo seguito, in ogni intorno di x₀ ci sono sia punti a_n su cui la funzione é positiva, sia punti b_n su cui la funzione é negativa, quindi l'unica possibilitá di non contraddire il teorema dei valori intermedi é che sia

f(x₀)=0.