


Next: Sessione autunnale, primo appello
Up: No Title
Previous: Sessione straordinaria
Analisi Matematica I
(Prof. Stefani)
Prova scritta del 15/07/1998 A
Durata: ore 2
Cognome, nome, matricola
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte. Risposte
senza giustificazione non verranno ritenute valide. Ove richiesto, la risposta deve
essere data sul presente foglio
ES.1 (p.nti 8)
a) Determinare il carattere della seguente serie
Risposta
...
b) Definire il significato di
...
ES.2 (p.nti 8)
a) Determinare il dominio di f
Risposta
...
b) Determinare le equazioni degli eventuali asintoti
Risposta
...
c) Determinare gli eventuali punti di
discontinuita' e classificarli
Risposta
...
ES.3 (p.nti 10) Si consideri l'integrale improprio
a) Definire il significato della frase
"il precedente integrale converge".
...
b) Calcolare il piu' piccolo n intero
per cui l'integrale converge.
Risposta
...
c) Calcolare l'integrale del punto b)
......
Risposta
ES.4 (p.nti 8)
a) Giustificare l'affermazione f ha
massimo e minimo globali e calcolarli
Risposta
...
ORALE :
Prima di Sabato 18/7 ...
 Dopo Sabato 18/7 ...
Dopo Sabato 18/7 ...
Analisi Matematica I
(Prof. Stefani)
Prova scritta del 15/07/1998 B
Durata: ore 2
Cognome, nome, matricola
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte. Risposte
senza giustificazione non verranno ritenute valide. Ove richiesto, la risposta deve
essere data sul presente foglio
ES.1 (p.nti 8)
a) Determinare il carattere della seguente serie
Risposta
...
b) Definire il significato di :
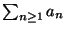 converge.
converge.
...
ES.2 (p.nti 8) sia
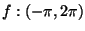 definita da
definita da
a) Determinare il dominio di f
Risposta
...
b) Determinare le equazioni degli eventuali asintoti
Risposta
...
c) Determinare gli eventuali punti di
discontinuita' e classificarli
Risposta
...
ES.3 (p.nti 10) Si consideri l'integrale improprio
a) Definire il significato della frase
"il precedente integrale converge".
...
b) Calcolare il piu' piccolo n intero
per cui l'integrale converge.
Risposta
...
c) Calcolare l'integrale del punto b)
......
Risposta
ES.4 (p.nti 8)
a) Giustificare l'affermazione f ha
massimo e minimo globali e calcolarli
Risposta
...
ORALE :
Prima di Sabato 18/7 ...
 Dopo Sabato 18/7 ...
Dopo Sabato 18/7 ...
Analisi Matematica I
(Prof. Stefani)
Prova scritta del 15/07/1998 C
Durata: ore 2
Cognome, nome, matricola
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte. Risposte
senza giustificazione non verranno ritenute valide. Ove richiesto, la risposta deve
essere data sul presente foglio
ES.1 (p.nti 8)
a) Determinare il carattere della seguente serie
Risposta
...
b) Definire il significato di
...
ES.2 (p.nti 8)
a) Determinare il dominio di f
Risposta
...
b) Determinare le equazioni degli eventuali asintoti
Risposta
...
c) Determinare gli eventuali punti di
discontinuita' e classificarli
Risposta
...
ES.3 (p.nti 10) Si consideri l'integrale improprio
a) Definire il significato della frase
"il precedente integrale converge".
...
b) Calcolare il piu' piccolo n intero
per cui l'integrale converge.
Risposta
...
c) Calcolare l'integrale del punto b)
......
Risposta
ES.4 (p.nti 8)
a) Giustificare
l'affermazione f ha massimo e minimo globali e calcolarli
Risposta
...
ORALE :
Prima di Sabato 18/7 ...
 Dopo Sabato 18/7 ...
Dopo Sabato 18/7 ...
Analisi Matematica I
(Prof. Stefani)
Prova scritta del 15/07/1998 D
Durata: ore 2
Cognome, nome, matricola
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte. Risposte
senza giustificazione non verranno ritenute valide. Ove richiesto, la risposta deve
essere data sul presente foglio
ES.1 (p.nti 8) a) Determinare il carattere della
seguente serie
Risposta
...
b)
Definire il significato di
...
ES.2 (p.nti 8) sia
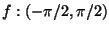 definita da
definita da
a) Determinare il dominio di f
Risposta
...
b) Determinare le equazioni degli eventuali asintoti
Risposta
...
c) Determinare gli eventuali punti di
discontinuita' e classificarli
Risposta
...
ES.3 (p.nti 10) Si consideri l'integrale improprio
a) Definire il significato della frase
"il precedente integrale converge".
...
b) Calcolare il piu' piccolo n intero
per cui l'integrale converge.
Risposta
...
c) Calcolare l'integrale del punto b)
......
Risposta
ES.4 (p.nti 8)
a) Giustificare l'affermazione f ha
massimo e minimo globali e calcolarli
Risposta
...
ORALE :
Prima di Sabato 18/7 ...
 Dopo Sabato 18/7 ...
Dopo Sabato 18/7 ...



Next: Sessione autunnale, primo appello
Up: No Title
Previous: Sessione straordinaria
Gianna Stefani
1998-12-03
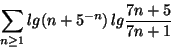
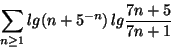
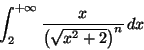
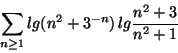
![\begin{displaymath}\int ^0_{-\infty}\frac{x^2}{\left(\sqrt[5]{2x^3+7}\right)^n}\,dx\end{displaymath}](img90.gif)
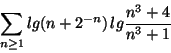
![\begin{displaymath}\int_7^{+\infty}\frac{x}{\left(\sqrt[7]{x^2-2}\right)^n}\,dx\end{displaymath}](img95.gif)
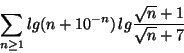
![\begin{displaymath}\int _ 1
^{-\infty}\frac{x^3}{\left(\sqrt[4]{x^4-1}\right)^n}\,dx\end{displaymath}](img101.gif)