Sessione straordinaria

Analisi Matematica I (Prof. Stefani) Prova scritta del 20/04/1998 ore 1

Cognome, nome, matricola

 
 
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte. Ove richiesto, se la risposta non e' riportata sul presente foglio, sara' giudicata incompleta. Risposte senza giustificazione non verranno ritenute valide.
 
ES.1 (p.nti 20)

$$\mbox {Sia} \hspace*{5cm} f(x)=e^{(x-1)\,ln\,\vert x+2\vert} \hspace*{5cm}$$

a) Determinare il dominio ed eventuali asintoti verticali orizzontali e obliqui
Risposta
...
...
...
b) f ha massimo o minimo assoluti?
Risposta
...
c) Giustificare l'affermazione: f ha massimo e minimo assoluti in [0,1]
Risposta
...
d) Calcolare la derivata prima
Risposta
...
e) Facoltativo Verificare che f e' crescente in 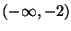$(-\infty,-2)$ ed ha un solo punto di minimo relativo che si trova in (-1,0)
...
f) Disegnare il grafico di f (usando anche il punto e)
...
g) Verificare che la parte di piano compresa fra il grafico di f il semiasse delle ascisse negative e la retta x=-5 ha area finita
...
h) Verificare che la precedente area e' minore di $\frac{1}{3^6}$
...
...
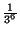
ES.2 (p.nti 10) Calcolare al variare di $\alpha\in {\bf R}\ ,\alpha >0$

$$\lim_{x\rightarrow +\infty} \left(cos\frac{1}{n^\alpha}\right)^n$$

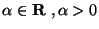
Risposta
...
...
...