


Next: Sessione straordinaria
Up: No Title
Previous: Sessione invernale, secondo appello
Analisi Matematica I
(Prof. Stefani)
Prova scritta del 24/02/1998 A
Durata: ore 2
Cognome, nome, matricola
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte.
Ove richiesto, se la risposta non e' riportata sul presente foglio,
sara' giudicata incompleta.
Risposte senza giustificazione non verranno ritenute valide.
ES.1 (p.nti 10)
a) Giustificare l'affermazione: f ha massimo e minimo in [1,3]
Risposta
...
b) Determinare il massimo e il minimo di cui al punto a) ed i valori della xin cui vengono raggiunti.
Risposta
...
ES.2 (p.nti 10)
Determinare al variare di
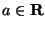 numero e segno delle radici reali del seguente
polinomio.
numero e segno delle radici reali del seguente
polinomio.
Risposta
...
...
...
b)Sul retro del presente foglio illustrare con un grafico la precedente risposta
...
ES.3 (p.nti 14) Sapendo che
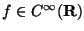 e che
e che
a) Determinare
f(4)(1)
Risposta
...
b) Determinare
f(5)(1)
Risposta
...
c) Quante derivate in x=1 posso determinare?
Risposta
...
d) Esprimere in forma di Lagrange
Risposta
......
Analisi Matematica I
(Prof. Stefani)
Prova scritta del 24/02/1998 B
Durata: ore 2
Cognome, nome, matricola
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte.
Ove richiesto, se la risposta non e' riportata sul presente foglio,
sara' giudicata incompleta.
Risposte
senza giustificazione non verranno ritenute valide.
ES.1 (p.nti 10)
Determinare al variare di
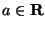 numero e segno delle radici reali del seguente
polinomio.
numero e segno delle radici reali del seguente
polinomio.
Risposta
...
...
...
b)Sul retro del presente foglio illustrare con un grafico la precedente risposta
...
ES.2 (p.nti 14)
a) Definire il significato di
Risposta
...
b) Verificare usando la definizione la precedente uguaglianza
......
c) Applicare il teorema della media integrale a
ed usarlo per verificare che
...
ES.3 (p.nti 10)
a) Giustificare l'affermazione: f ha massimo e minimo in
![$[\frac{1}{2},2]$](img67.gif)
Risposta
...
b) Determinare il massimo e il minimo di cui al punto a) ed i valori della xin cui vengono raggiunti.
Risposta
...
Analisi Matematica I
(Prof. Stefani)
Prova scritta del 24/02/1998 C
Durata: ore 2
Cognome, nome, matricola
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte.
Ove richiesto, se la risposta non e' riportata sul presente foglio,
sara' giudicata incompleta.
Risposte
senza giustificazione non verranno ritenute valide.
ES.1 (p.nti 10)
a) Giustificare l'affermazione: f ha massimo e minimo in [-3,-1]
Risposta
...
b) Determinare il massimo e il minimo di cui al punto a) ed i valori della xin cui vengono raggiunti.
Risposta
...
ES.2 (p.nti 10)
Determinare al variare di
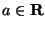 numero e segno delle radici reali del seguente
polinomio.
numero e segno delle radici reali del seguente
polinomio.
Risposta
...
...
...
b)Sul retro del presente foglio illustrare con un grafico la precedente risposta
...
ES.3 (p.nti 14) Sapendo che
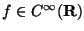 e che
e che
a) Determinare
f(3)(0)
Risposta
...
b) Quante derivate di (f(x))2 in x=0 posso determinare?
Risposta
...
c) Esprimere in forma di Lagrange
f(1)-1-1/3
Risposta
......
Analisi Matematica I
(Prof. Stefani)
Prova scritta del 24/02/1998 D
Durata: ore 2
Cognome, nome, matricola
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte.
Ove richiesto, se la risposta non e' riportata sul presente foglio,
sara' giudicata incompleta.
Risposte
senza giustificazione non verranno ritenute valide.
ES.1 (p.nti 10)
Determinare al variare di
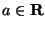 numero e segno delle radici reali del seguente
polinomio.
numero e segno delle radici reali del seguente
polinomio.
Risposta
...
...
...
b)Sul retro del presente foglio illustrare con un grafico la precedente risposta
...
ES.2 (p.nti 10)
a) Giustificare l'affermazione: f ha massimo e minimo in [-1,11]
Risposta
...
b) Determinare il massimo e il minimo di cui al punto a) ed i valori della xin cui vengono raggiunti.
Risposta
...
ES.3 (p.nti 14)
a) Definire il significato di
Risposta
...
b) Verificare usando la definizione la precedente uguaglianza
......
c) Applicare il teorema della media integrale a
ed usarlo per verificare che
...



Next: Sessione straordinaria
Up: No Title
Previous: Sessione invernale, secondo appello
Gianna Stefani
1998-12-03