


Next: Sessione invernale, terzo appello
Up: No Title
Previous: Sessione invernale, primo appello
Analisi Matematica I
(Prof. Stefani)
Prova scritta del 05/02/1998 A
Durata: ore 2
Cognome, nome, matricola
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte.
Risposte non riportate sul presente foglio saranno giudicate incomplete. Risposte
senza giustificazione non verranno ritenute valide.
ES.1 (p.nti 10)
Determinare il massimo k per cui
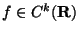
Risposta
...
ES.2 (p.nti 14) Sia
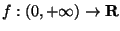 definita da
definita da
a) Determinare la tangente al grafico di fnel punto di ascissa 1
Risposta
...
b) Calcolare
Risposta
...
c) La funzione ha un asintoto destro (orizzontale o obliquo)?
Risposta
...
d) Facoltativo. La f e' prolungabile per continuita' a 0?
Risposta
...
ES.3 (p.nti 10) a) Se la serie
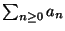 converge cosa possiamo affermare sul carattere
della successione an?
converge cosa possiamo affermare sul carattere
della successione an?
Risposta
...
b) Usare la condizione per verificare che la serie
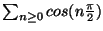 non converge.
non converge.
...
...
ORALE :
9/02/98 e seguenti ...
 III appello ...
III appello ...
Analisi Matematica I
(Prof. Stefani)
Prova scritta del 05/02/1998 B
Durata: ore 2
Cognome, nome, matricola
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte.
Risposte non riportate sul presente foglio saranno giudicate incomplete. Risposte
senza giustificazione non verranno ritenute valide.
ES.1 (p.nti 14) Sia
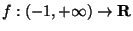 definita da
definita da
a) Determinare la tangente al grafico di fnel punto di ascissa 0
Risposta
...
b) Calcolare
Risposta
...
c) La funzione ha un asintoto destro (orizzontale o obliquo)?
Risposta
...
d) Facoltativo. La retta x=-1 e' un asintoto per la funzione?
Risposta
...
ES.2 (p.nti 10)
Determinare il massimo k per cui
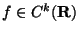
Risposta
...
ES.3 (p.nti 10) Definire il significato di:
la serie
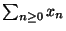 e' indeterminata.
e' indeterminata.
Usare la definizione per verificare che la serie
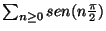 e' indeterminata.
e' indeterminata.
...
...
ORALE :
9/02/98 e seguenti ...
 III appello ...
III appello ...
Analisi Matematica I
(Prof. Stefani)
Prova scritta del 05/02/1998 C
Durata: ore 2
Cognome, nome, matricola
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte.
Risposte non riportate sul presente foglio saranno giudicate incomplete. Risposte
senza giustificazione non verranno ritenute valide.
ES.1 (p.nti 10) Definire il significato di :
la serie
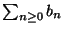 diverge a
diverge a 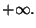
Usare la definizione per verificare che la serie
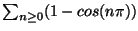 diverge a
diverge a 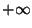 .
.
...
ES.2 (p.nti 10)
Determinare il massimo k per cui
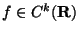
Risposta
...
ES.3 (p.nti 14) Sia
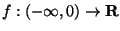 definita da
definita da
a) Determinare la tangente al grafico di fnel punto di ascissa -1
Risposta
...
b) Calcolare
Risposta
...
c) La funzione ha un asintoto sinistro (orizzontale o obliquo)?
Risposta
...
d) La f e' prolungabile per continuita' a 0?
Risposta
...
...
ORALE :
9/02/98 e seguenti ...
 III appello ...
III appello ...
Analisi Matematica I
(Prof. Stefani)
Prova scritta del 05/02/1998 D
Durata: ore 2
Cognome, nome, matricola
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte.
Risposte non riportate sul presente foglio saranno giudicate incomplete. Risposte
senza giustificazione non verranno ritenute valide.
ES.1 (p.nti 14) Sia
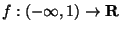 definita da
definita da
a) Determinare la tangente al grafico di fnel punto di ascissa 0
Risposta
...
b) Calcolare
Risposta
...
c) La funzione ha un asintoto sinistro (orizzontale o obliquo)?
Risposta
...
d) La retta x=1 e' un asintoto per la funzione?
Risposta
...
ES.2 (p.nti 10) Definire il significato di:
la serie
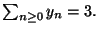
Usare la definizione per verificare che la serie
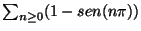 non converge a 3.
non converge a 3.
...
ES.3 (p.nti 10)
Determinare il massimo k per cui
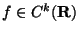
Risposta
...
...
ORALE :
9/02/98 e seguenti ...
 III appello ...
III appello ...



Next: Sessione invernale, terzo appello
Up: No Title
Previous: Sessione invernale, primo appello
Gianna Stefani
1998-12-03