


Next: Sessione invernale, secondo appello
Up: No Title
Previous: No Title
Analisi Matematica I
(Prof. Stefani)
Prova scritta del 14/01/1998 A
Durata: ore 2
Cognome, nome, matricola
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte. Risposte
senza giustificazione non verranno ritenute valide.
ES.1 (p.nti 10)
a) determinare per quali valori di
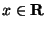 la serie e' assolutamente
convergente
la serie e' assolutamente
convergente
Risposta
...
b) determinare per quali valori di
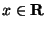 la serie e' convergente
la serie e' convergente
Risposta
...
ES.2 (p.nti 14)
a) Determinare il dominio di f
Risposta
...
b) Determinare la tangente al grafico nel punto di ascissa 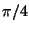
Risposta
...
c) Determinare le equazioni degli asintoti
Risposta
...
d) Determinare i punti di max e min relativo
Risposta
......
e) Disegnare sul retro il grafico della funzione
...
f) Determinare massimo e
minimo di
![$f_{\vert[\frac{\pi}{4} ,\frac{5\pi}{6}]}$](img5.gif)
Risposta
......
g) L'area compresa fra il grafico della funzione,
l' asse x, e le rette
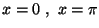 e' finita?
e' finita?
Risposta
...
h) Facoltativo. Usando il grafico di fed il precedente punto g), disegnare sul retro il grafico di
...
ES.3 (p.nti 10) Dare la definizione di
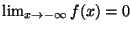 e verificare, usando la definizione, che
e verificare, usando la definizione, che
...
...
ORALE :
prima del 20/01/98 ...
 II appello ...
II appello ...
Analisi Matematica I
(Prof. Stefani)
Prova scritta del 14/01/1998 B
Durata: ore 2
Cognome, nome, matricola
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte. Risposte
senza giustificazione non verranno ritenute valide.
ES.1 (p.nti 14)
a) Determinare il dominio di f
Risposta
...
b) Determinare le equazioni degli asintoti
Risposta
...
c) Determinare i punti di max e min relativo
Risposta
......
d) Disegnare sul retro il grafico della funzione
...
e) Determinare la tangente al grafico nel punto di ascissa 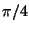
Risposta
...
f) Determinare massimo e
minimo di
![$f_{\vert[-\frac{\pi}{3} ,\frac{\pi}{4}]}$](img13.gif)
Risposta
......
g) L'area compresa fra il grafico della funzione,
l' asse x, e le rette
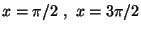 e' finita?
e' finita?
Risposta
...
h) Facoltativo. Usando il grafico di fed il precedente punto g), disegnare sul retro il grafico di
...
ES.2 (p.nti 10)
a) determinare per quali valori di
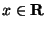 la serie e' assolutamente
convergente
la serie e' assolutamente
convergente
Risposta
...
b) determinare per quali valori di
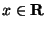 la serie e' convergente
la serie e' convergente
Risposta
...
ES.3 (p.nti 10) Dare la definizione di
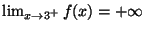 e verificare, usando la definizione, che
e verificare, usando la definizione, che
...
...
ORALE :
prima del 20/01/98 ...
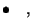 II appello ...
II appello ...
Analisi Matematica I
(Prof. Stefani)
Prova scritta del 14/01/1998 C
Durata: ore 2
Cognome, nome, matricola
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte. Risposte
senza giustificazione non verranno ritenute valide.
ES.1 (p.nti 10)
a) determinare per quali valori di
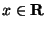 la serie e' assolutamente
convergente
la serie e' assolutamente
convergente
Risposta
...
b) determinare per quali valori di
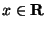 la serie e' convergente
la serie e' convergente
Risposta
...
ES.2 (p.nti 14)
a) Determinare il dominio di f
Risposta
...
b) Determinare la tangente al grafico nel punto di ascissa 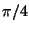
Risposta
...
c) Determinare le equazioni degli asintoti
Risposta
...
d) Determinare i punti di max e min relativo
Risposta
......
e) Disegnare sul retro il grafico della funzione
...
f) Determinare massimo e
minimo di
![$f_{\vert[-\frac{\pi}{6} ,\frac{\pi}{4}]}$](img21.gif)
Risposta
......
g) L'area compresa fra il grafico della funzione,
l' asse x, e le rette
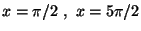 e' finita?
e' finita?
Risposta
...
h) Facoltativo. Usando il grafico di fed il precedente punto g), disegnare sul retro il grafico di
...
ES.3 (p.nti 10) Dare la definizione di
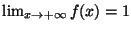 e verificare, usando la definizione, che
e verificare, usando la definizione, che
...
...
ORALE :
prima del 20/01/98 ...
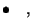 II appello ...
II appello ...
Analisi Matematica I
(Prof. Stefani)
Prova scritta del 14/01/1998 D
Durata: ore 2
Cognome, nome, matricola
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte. Risposte
senza giustificazione non verranno ritenute valide.
ES.1 (p.nti 14)
a) Determinare il dominio di f
Risposta
...
b) Determinare le equazioni degli asintoti
Risposta
...
c) Determinare i punti di max e min relativo
Risposta
......
d) Disegnare sul retro il grafico della funzione
...
e) Determinare la tangente al grafico nel punto di ascissa 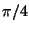
Risposta
...
f) Determinare massimo e
minimo di
![$f_{\vert[\frac{\pi}{6} ,\frac{5\pi}{6}]}$](img26.gif)
Risposta
......
g) L'area compresa fra il grafico della funzione,
l' asse x, e le rette
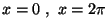 e' finita?
e' finita?
Risposta
...
h) Facoltativo. Usando il grafico di fed il precedente punto g), disegnare sul retro il grafico di
...
ES.2 (p.nti 10)
a) determinare per quali valori di
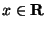 la serie e' assolutamente
convergente
la serie e' assolutamente
convergente
Risposta
...
b) determinare per quali valori di
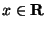 la serie e' convergente
la serie e' convergente
Risposta
...
ES.3 (p.nti 10) Dare la definizione di
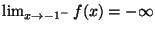 e verificare, usando la definizione, che
e verificare, usando la definizione, che
...
...
ORALE :
prima del 20/01/98 ...
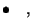 II appello ...
II appello ...



Next: Sessione invernale, secondo appello
Up: No Title
Previous: No Title
Gianna Stefani
1998-12-03