


Next: Variabili aleatorie indipendenti
Up: Variabili aleatorie.
Previous: Variabili aleatorie discrete
Spesso è necessario considerare simultaneamente più variabili aleatorie.
Definizione 2.2.1. Si chiama vettore aleatorio o
var.al. 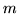 -dimensionale un vettore
-dimensionale un vettore
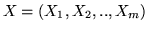 ,
le cui componenti
,
le cui componenti 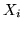 siano var.al. nel senso della defin. 2.1.1.
siano var.al. nel senso della defin. 2.1.1.
La densità 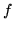 di
di  si definisce allo stesso modo, cioè
si definisce allo stesso modo, cioè
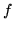 viene anche detta densità congiunta delle
viene anche detta densità congiunta delle 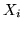 le cui densità,
dette marginali, possono essere indicate con
le cui densità,
dette marginali, possono essere indicate con 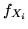 . Se si conosce la
densità congiunta si possono calcolare le densità marginali; per
semplicità trattiamo il caso
. Se si conosce la
densità congiunta si possono calcolare le densità marginali; per
semplicità trattiamo il caso 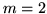 . Sia
. Sia 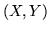 una
var.al. 2-dimensionale con densità
una
var.al. 2-dimensionale con densità 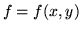 . Indichiamo con
. Indichiamo con
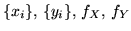 i valori possibili e le densità di
i valori possibili e le densità di
 e
e 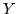 rispett. Si ha
rispett. Si ha
Analogamente si ha
Non basta invece
conoscere le densità marginali per calcolare la densità
congiunta, perchè densità congiunte diverse possono avere
densità marginali uguali.
Del resto è chiaro che anche avendo tutti i dati relativi a una var.al.  e a un'altra var.al.
e a un'altra var.al. 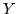 (per esempio la conoscenza delle rispettive densità
(per esempio la conoscenza delle rispettive densità
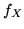 e
e 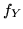 ) nulla si può sapere sulle probabilità che si realizzino
simultaneamente un evento concernente la var.al.
) nulla si può sapere sulle probabilità che si realizzino
simultaneamente un evento concernente la var.al.  e un altro concernente la
e un altro concernente la 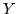 ; questo a meno che non si sappia a priori che
; questo a meno che non si sappia a priori che  e
e 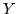 sono var.al. indipendenti
(vedi dopo).
sono var.al. indipendenti
(vedi dopo).



Next: Variabili aleatorie indipendenti
Up: Variabili aleatorie.
Previous: Variabili aleatorie discrete
Stefani Gianna
2000-11-06
![]() di
di ![]() si definisce allo stesso modo, cioè
si definisce allo stesso modo, cioè