


Next: Caso vettoriale
Up: Variabili aleatorie.
Previous: Variabili aleatorie.
Definizione 2.1.1. Una funzione
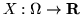 , dove
, dove
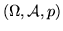 è uno spazio di
probabilità, si dice che è una variabile aleatoria (var.al.) se per
ogni
è uno spazio di
probabilità, si dice che è una variabile aleatoria (var.al.) se per
ogni 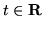 ,
,
Questa denominazione è un po' fuorviante: occorrerebbe dire
funzione aleatoria e non var.al.; tuttavia è ormai
divenuta standard.
Tipici esempi di var.al.: il numero di successi in 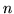 prove di Bernoulli (vedi dopo), il guadagno (o perdita) di uno scommettitore in
un gioco d'azzardo.
prove di Bernoulli (vedi dopo), il guadagno (o perdita) di uno scommettitore in
un gioco d'azzardo.
Considereremo qui solo var.al. discrete:
supporremo cioè che la var.al.  prenda al più un insieme numerabile di
valori distinti
prenda al più un insieme numerabile di
valori distinti
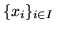 dove l'insieme
dove l'insieme 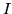 degli indici
è finito o numerabile.
degli indici
è finito o numerabile.
Definizione 2.1.2. Data la var.al.  , la sua densità
(discreta) è la funzione
, la sua densità
(discreta) è la funzione
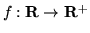
Si osservi che
i) 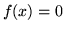 se
se 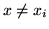 ,
,
ii)
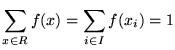 .
.
Ogni funzione
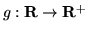 che soddisfi i) e ii) viene
chiamata densità.
che soddisfi i) e ii) viene
chiamata densità.
Scriveremo poi di solito
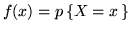 anzichè più correttamente
anzichè più correttamente
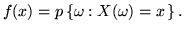
Consideriamo ora un esempio importante: il così detto
Schema di Bernoulli : Una prova (ad es. lancio di moneta) ha
due soli possibili risultati: successo (T) con probabilità 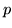 e
insuccesso (C) con probabilità
e
insuccesso (C) con probabilità 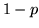 . Consideriamo il caso che si ripetano
. Consideriamo il caso che si ripetano
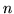 prove di questo tipo. Le
prove di questo tipo. Le 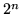 sequenze distinte
che si possono formare con i simboli T e C sono uno spazio di campioni
sequenze distinte
che si possono formare con i simboli T e C sono uno spazio di campioni 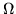 . Sia
. Sia
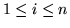 ; siano
; siano 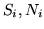 gli eventi ``T all'i-ma prova", ``C all'i-ma
prova" rispett. Qualunque sia
gli eventi ``T all'i-ma prova", ``C all'i-ma
prova" rispett. Qualunque sia 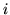 si ha
si ha
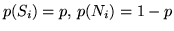 ; inoltre se gli
indici sono tutti distinti, ogni gruppo di eventi del tipo
; inoltre se gli
indici sono tutti distinti, ogni gruppo di eventi del tipo 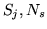 costituisce
una famiglia di eventi indipendenti.
costituisce
una famiglia di eventi indipendenti.
Teorema 2.1.1. Se
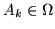 è l'evento ``
è l'evento ``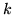 successi negli
successi negli 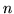 lanci", allora
lanci", allora
Dimostrazione. Una sequenza con 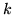 successi (e quindi
successi (e quindi 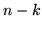 insuccessi) si ottiene come intersezione di
insuccessi) si ottiene come intersezione di 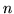 eventi:
eventi: 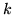 di tipo
di tipo
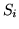 e
e 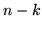 di tipo
di tipo 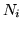 , a causa dell'indipendenza questa
sequenza ha probabilità
, a causa dell'indipendenza questa
sequenza ha probabilità
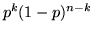 . Si conclude notando
che di tali sequenze ce ne sono
. Si conclude notando
che di tali sequenze ce ne sono 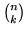 .
.
Indichiamo con 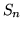 il numero di successi in
il numero di successi in 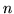 prove di Bernoulli.
prove di Bernoulli. 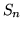 è una var.al. definita su
è una var.al. definita su 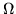 : se
: se
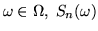 è il numero di volte che compare
è il numero di volte che compare 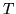 nella sequenza
nella sequenza 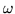 ; i valori
possibili di
; i valori
possibili di 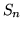 sono 0,1,..,
sono 0,1,..,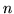 . Per la densità
. Per la densità 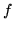 di
di 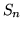 si ha
si ha
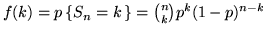 per
per 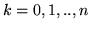 e 0 altrimenti; cioè
e 0 altrimenti; cioè 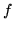 è concentrata nell'insieme
è concentrata nell'insieme
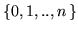 che a volte per brevità si prende come dominio di
che a volte per brevità si prende come dominio di 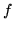 omettendo di
definire la densità dove è 0.
omettendo di
definire la densità dove è 0.
Vedremo che è possibile fare calcoli significativi con le probabilità
anche senza considerare esplicitamente lo spazio dei campioni.
Si noti infine che
dove 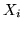 è la var.al che vale 1 se all'i-ma prova si ha successo e 0 se si ha
insuccesso (la sua densità vale risp.
è la var.al che vale 1 se all'i-ma prova si ha successo e 0 se si ha
insuccesso (la sua densità vale risp. 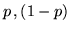 e 0 in ogni altro
caso).
e 0 in ogni altro
caso).
Diremo che 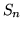 segue una legge binomiale di
parametri
segue una legge binomiale di
parametri 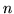 e
e 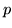 che si indica con
che si indica con 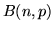 . Chiaramente ogni
. Chiaramente ogni 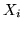 ha legge
ha legge
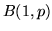 .
.
Definizione 2.1.4. Data una var.al.  si chiama
funzione di ripartizione (f.r.) la funzione
si chiama
funzione di ripartizione (f.r.) la funzione
![$F_X : {\bf R} \rightarrow [0,1]$](img251.gif) definita da
definita da
Una f.r. è sempre non decrescente. Se 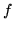 è la
densità di
è la
densità di  , si ha
, si ha
se  prende valori
interi si ha pure
prende valori
interi si ha pure



Next: Caso vettoriale
Up: Variabili aleatorie.
Previous: Variabili aleatorie.
Stefani Gianna
2000-11-06
![]() prove di Bernoulli (vedi dopo), il guadagno (o perdita) di uno scommettitore in
un gioco d'azzardo.
prove di Bernoulli (vedi dopo), il guadagno (o perdita) di uno scommettitore in
un gioco d'azzardo.
![]() prenda al più un insieme numerabile di
valori distinti
prenda al più un insieme numerabile di
valori distinti
![]() dove l'insieme
dove l'insieme ![]() degli indici
è finito o numerabile.
degli indici
è finito o numerabile. ![]() , la sua densità
(discreta) è la funzione
, la sua densità
(discreta) è la funzione
![]()
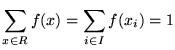 .
.
![]() il numero di successi in
il numero di successi in ![]() prove di Bernoulli.
prove di Bernoulli. ![]() è una var.al. definita su
è una var.al. definita su ![]() : se
: se
![]() è il numero di volte che compare
è il numero di volte che compare ![]() nella sequenza
nella sequenza ![]() ; i valori
possibili di
; i valori
possibili di ![]() sono 0,1,..,
sono 0,1,..,![]() . Per la densità
. Per la densità ![]() di
di ![]() si ha
si ha
![]() per
per ![]() e 0 altrimenti; cioè
e 0 altrimenti; cioè ![]() è concentrata nell'insieme
è concentrata nell'insieme
![]() che a volte per brevità si prende come dominio di
che a volte per brevità si prende come dominio di ![]() omettendo di
definire la densità dove è 0.
omettendo di
definire la densità dove è 0.