


Next: Esercizi e complementi
Up: Lo spazio di probabilità.
Previous: Esempi.
Un gruppo 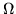 di
di 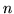 persone atte al lavoro contiene
persone atte al lavoro contiene 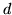 disoccupati e
disoccupati e 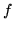 femmine. Si sceglie una persona a caso dal gruppo,
sia
femmine. Si sceglie una persona a caso dal gruppo,
sia 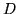 l'evento ``disoccupato" e
l'evento ``disoccupato" e 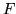 l'evento ``femmina", allora
l'evento ``femmina", allora
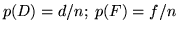 . Se consideriamo il sottogruppo delle femmine,
scegliendone una a caso, la probabilità che sia disoccupata è
. Se consideriamo il sottogruppo delle femmine,
scegliendone una a caso, la probabilità che sia disoccupata è
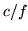 dove
dove 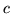 è il numero di disoccupati femmine. Possiamo
esprimerci così:
è il numero di disoccupati femmine. Possiamo
esprimerci così: 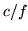 è la probabilità che si verifichi
l'evento
è la probabilità che si verifichi
l'evento 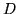 assumendo che si sia verificato l'evento
assumendo che si sia verificato l'evento 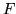 . Useremo la
notazione
. Useremo la
notazione 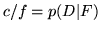 che leggeremo: ``probabilità condizionale
di
che leggeremo: ``probabilità condizionale
di 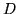 rispetto a
rispetto a 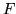 ". Osserviamo subito che, poichè
". Osserviamo subito che, poichè
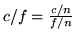 , vale la formula
, vale la formula
Si può considerare 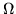 come uno spazio con probabilità
uniforme (
come uno spazio con probabilità
uniforme (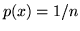 su ogni atomo
su ogni atomo 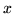 ) definita su tutti i
sottoinsiemi. La probabilità condizionale
) definita su tutti i
sottoinsiemi. La probabilità condizionale
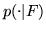 è
un'altra probabilità su
è
un'altra probabilità su 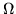 che assegna probabilità
0 agli eventi disgiunti da
che assegna probabilità
0 agli eventi disgiunti da 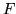 ; oppure si può vederla come
una probabilità sullo spazio
; oppure si può vederla come
una probabilità sullo spazio 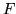 . Come si vede la
probabilità condizionale non è un concetto nuovo, tuttavia
risulta un modo utile di muoversi per risolvere un problema. Sia
. Come si vede la
probabilità condizionale non è un concetto nuovo, tuttavia
risulta un modo utile di muoversi per risolvere un problema. Sia
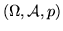 uno spazio di probabilità,
diamo la formale
uno spazio di probabilità,
diamo la formale
Definizione 1.3.1 Siano
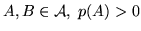 . Si
chiama probabilità condizionale di
. Si
chiama probabilità condizionale di 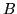 rispetto ad
rispetto ad 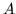 la
quantità
la
quantità
Come esempio consideriamo le famiglie che hanno esattamente due
bambini, scriviamo 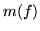 per maschio (femmina) e la prima lettera
rappresenta il primogenito. Su
per maschio (femmina) e la prima lettera
rappresenta il primogenito. Su
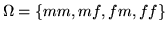 consideriamo la probabilità uniforme (
consideriamo la probabilità uniforme (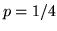 su ogni
atomo). Sapendo che una famiglia ha un maschio (evento
su ogni
atomo). Sapendo che una famiglia ha un maschio (evento 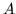 ), qual'
è la probabilità dell'evento
), qual'
è la probabilità dell'evento 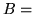 ``figli entrambi maschi"?
Poichè
``figli entrambi maschi"?
Poichè
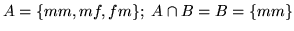 , si ha che la
probabilità richiesta
, si ha che la
probabilità richiesta 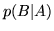 vale
vale
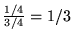 .
(Si noti che un esame diretto dello spazio dei campioni porta
immediatamente a questo risultato).
.
(Si noti che un esame diretto dello spazio dei campioni porta
immediatamente a questo risultato).
Consideriamo ora una partizione 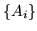 di uno spazio
di probabilità
di uno spazio
di probabilità 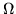 , per ogni altro evento
, per ogni altro evento 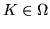 vale la
vale la
Formula di Bayes
Dimostrazione. Basta osservare che
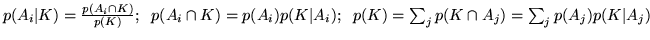 .
.
Esempio. Supponiamo che in una famiglia la probabilità che
ci siano 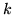 figli sia
figli sia
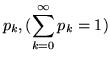 ; supponiamo
inoltre che la distribuzione dei sessi sia uniforme. Sapendo che non ci sono
femmine (evento
; supponiamo
inoltre che la distribuzione dei sessi sia uniforme. Sapendo che non ci sono
femmine (evento 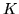 ), qual'è la probabilità (condizionale) che
nella famiglia ci siano esattamente
), qual'è la probabilità (condizionale) che
nella famiglia ci siano esattamente 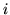 figli (evento
figli (evento 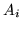 )? Abbiamo:
)? Abbiamo:
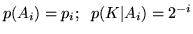 , per la formula di Bayes
la probabilità richiesta è:
, per la formula di Bayes
la probabilità richiesta è:
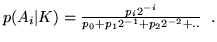
``Filosofia" della formula di Bayes. Se chiamiamo
``cause" gli eventi 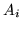 che compaiono nella formula di Bayes,
allora si può interpretare la formula come una regola per calcolare
a posteriori la probabilità che
che compaiono nella formula di Bayes,
allora si può interpretare la formula come una regola per calcolare
a posteriori la probabilità che 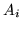 sia stato
la causa dell'essersi verificato l'evento
sia stato
la causa dell'essersi verificato l'evento 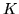 . Per questo motivo la
formula di Bayes viene molto usata in statistica; tuttavia se si usa a
questo scopo la formula occorre molta cautela nell'interpretarne
i risultati.
. Per questo motivo la
formula di Bayes viene molto usata in statistica; tuttavia se si usa a
questo scopo la formula occorre molta cautela nell'interpretarne
i risultati.
La probabilità (condizionale) 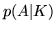 è in generale diversa
dalla probabilità (assoluta)
è in generale diversa
dalla probabilità (assoluta) 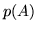 , intuitivamente:
l'informazione che l'evento
, intuitivamente:
l'informazione che l'evento 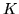 si è verificato cambia la nostra
maniera di scommettere sul verificarsi dell'evento
si è verificato cambia la nostra
maniera di scommettere sul verificarsi dell'evento 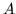 . Quando
. Quando 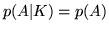 è un po' come dire che l'evento
è un po' come dire che l'evento 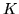 non influenza
(è indipendente dal) l'evento
non influenza
(è indipendente dal) l'evento 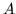 ; questo caso si ha se e
solo se vale l'uguaglianza
; questo caso si ha se e
solo se vale l'uguaglianza
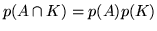 e si vede quindi
che se
e si vede quindi
che se 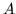 è indipendente da
è indipendente da 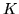 allora
allora 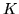 è indipendente da
è indipendente da
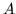 . Diamo dunque la fondamentale
. Diamo dunque la fondamentale
Definizione 1.3.2 Due eventi 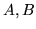 si dicono
(stocasticamente) indipendenti se
si dicono
(stocasticamente) indipendenti se
Una famiglia di eventi 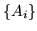 si dice indipendente se per ogni
gruppo di
si dice indipendente se per ogni
gruppo di 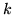 indici distinti si ha
indici distinti si ha
Se una moneta viene lanciata ripetutamente, accettiamo di ritenere
che l'esito di un lancio non influenza l'esito di un altro lancio
(per es. il successivo), ciò si riflette nella (stocastica)
indipendenza di alcuni eventi.



Next: Esercizi e complementi
Up: Lo spazio di probabilità.
Previous: Esempi.
Stefani Gianna
2000-11-06
![]() per maschio (femmina) e la prima lettera
rappresenta il primogenito. Su
per maschio (femmina) e la prima lettera
rappresenta il primogenito. Su
![]() consideriamo la probabilità uniforme (
consideriamo la probabilità uniforme (![]() su ogni
atomo). Sapendo che una famiglia ha un maschio (evento
su ogni
atomo). Sapendo che una famiglia ha un maschio (evento ![]() ), qual'
è la probabilità dell'evento
), qual'
è la probabilità dell'evento ![]() ``figli entrambi maschi"?
Poichè
``figli entrambi maschi"?
Poichè
![]() , si ha che la
probabilità richiesta
, si ha che la
probabilità richiesta ![]() vale
vale
![]() .
(Si noti che un esame diretto dello spazio dei campioni porta
immediatamente a questo risultato).
.
(Si noti che un esame diretto dello spazio dei campioni porta
immediatamente a questo risultato).
![]() di uno spazio
di probabilità
di uno spazio
di probabilità ![]() , per ogni altro evento
, per ogni altro evento ![]() vale la
vale la 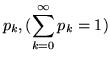 ; supponiamo
inoltre che la distribuzione dei sessi sia uniforme. Sapendo che non ci sono
femmine (evento
; supponiamo
inoltre che la distribuzione dei sessi sia uniforme. Sapendo che non ci sono
femmine (evento