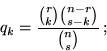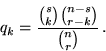Qui
Collocamento a caso di ![]() palle in
palle in ![]() celle.
celle.
Qui ![]() ed
ed ![]() sono numeri naturali positivi. Esistono
sono numeri naturali positivi. Esistono
![]() arrangiamenti possibili, a ciascuno dei quali attribuiremo
probabilità
arrangiamenti possibili, a ciascuno dei quali attribuiremo
probabilità ![]() (basta osservare che per la prima
palla ci sono
(basta osservare che per la prima
palla ci sono ![]() scelte, altrettante per la seconda, la terza e
così via). Ecco degli esempi concreti:
scelte, altrettante per la seconda, la terza e
così via). Ecco degli esempi concreti:
Totocalcio. Le ``![]() palle" sono le 13 partite, le
``
palle" sono le 13 partite, le
``![]() celle" sono i tre possibili risultati 1, x, 2 degli incontri.
Se per ogni partita 1, x, 2 sono equiprobabili
(ipotesi non realistica), allora la
probabilità di ``fare 13", cioè di indovinare tutti i
risultati, vale
celle" sono i tre possibili risultati 1, x, 2 degli incontri.
Se per ogni partita 1, x, 2 sono equiprobabili
(ipotesi non realistica), allora la
probabilità di ``fare 13", cioè di indovinare tutti i
risultati, vale
![]() .
.
![]() lanci di monete. Le ``
lanci di monete. Le ``![]() palle" sono gli
palle" sono gli ![]() lanci,
le ``
lanci,
le ``![]() celle" sono i 2 risultati T e C. Se in ogni lancio T e C
hanno probabilità 1/2, allora le
celle" sono i 2 risultati T e C. Se in ogni lancio T e C
hanno probabilità 1/2, allora le ![]() sequenze possibili di
risultati sono equiprobabili, per es. la probabilità di una
sequenza tutta di teste vale
sequenze possibili di
risultati sono equiprobabili, per es. la probabilità di una
sequenza tutta di teste vale ![]() .
.
Compleanni. Le ``![]() palle" sono
palle" sono ![]() persone scelte a
caso, le ``
persone scelte a
caso, le ``![]() celle" sono i 365 giorni dell'anno. Se
si considera equiprobabile ogni data, allora ogni
distribuzione di compleanni di
celle" sono i 365 giorni dell'anno. Se
si considera equiprobabile ogni data, allora ogni
distribuzione di compleanni di ![]() persone ha probabilità
persone ha probabilità
![]() . Consideriamo il seguente problema: quanto vale la
probabilità
. Consideriamo il seguente problema: quanto vale la
probabilità ![]() dell'evento
dell'evento ![]() = ``nel gruppo almeno due
persone hanno il compleanno nello stesso giorno" ?
= ``nel gruppo almeno due
persone hanno il compleanno nello stesso giorno" ?
Calcoliamo la probabilità dell'evento complementare ![]() =
``le persone del gruppo hanno il compleanno in giorni tutti
distinti". Per la prima persona si può scegliere in 365 modi,
per la seconda in 364, per la terza in 363 e così via. Le
scelte possibili sono
=
``le persone del gruppo hanno il compleanno in giorni tutti
distinti". Per la prima persona si può scegliere in 365 modi,
per la seconda in 364, per la terza in 363 e così via. Le
scelte possibili sono
![]() e quindi
e quindi
Estrazione con rimpiazzamento. Le ``![]() palle" sono
palle" sono
![]() palle estratte a caso da un'urna contenente
palle estratte a caso da un'urna contenente ![]() palle chiamate
``1", ``2",..,``n" (dopo ogni estrazione la palla estratta viene reintrodotta
nell'urna), le ``
palle chiamate
``1", ``2",..,``n" (dopo ogni estrazione la palla estratta viene reintrodotta
nell'urna), le ``![]() celle" sono gli
celle" sono gli ![]() nomi delle palle nell'urna. Con
nomi delle palle nell'urna. Con ![]() estrazioni si possono ottenere
estrazioni si possono ottenere ![]() campioni distinti.
campioni distinti.
Consideriamo ora un problema un po' più complesso.
Distribuzione ipergeometrica. In una popolazione di
![]() individui ce ne sono
individui ce ne sono ![]() rossi (
rossi (![]() ); si scelgono
a caso
); si scelgono
a caso ![]() individui (
individui (![]() ), determinare la probabilità
), determinare la probabilità
![]() che questo gruppo contenga esattamente
che questo gruppo contenga esattamente ![]() individui rossi
(
individui rossi
(
![]() ). Dal gruppo dei rossi si possono
scegliere
). Dal gruppo dei rossi si possono
scegliere ![]() individui in
individui in ![]() modi, gli altri
modi, gli altri
![]() in
in
![]() modi; pertanto
modi; pertanto