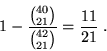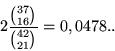Next: Variabili aleatorie.
Up: Lo spazio di probabilità.
Previous: Probabilità condizionale, indipendenza.
1. Generalizzare il Teorema 1.1.1 a tre e poi a  eventi.
eventi.
Abbiamo successivamente:
Per generalizzare a  eventi
eventi  poniamo:
poniamo:
Si può dimostrare che la probabilità  che si verifichi uno almeno degli
eventi
che si verifichi uno almeno degli
eventi 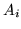 vale
vale
2. Problema dei matches .
Un mazzo di 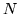 carte numerate
carte numerate 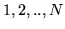 viene mescolato e steso in fila su un
tavolo. Agli
viene mescolato e steso in fila su un
tavolo. Agli 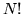 ordinamenti possibili delle carte viene assegnata la
probabilità
ordinamenti possibili delle carte viene assegnata la
probabilità 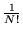 . Si chiede il valore della probabilità
. Si chiede il valore della probabilità 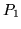 che
almeno una carta sia al posto giusto (carta denotata
che
almeno una carta sia al posto giusto (carta denotata 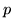 al posto
al posto 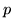 -mo).
-mo).
Soluzione.
Se c'è un match all'i-mo posto, le rimanenti carte possono essere disposte in
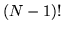 modi per cui per la corrispondente probabilità si ha
modi per cui per la corrispondente probabilità si ha
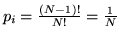 , similmente per la probabilità di match
simultaneo al posto i e al posto (distinto) j si ha
, similmente per la probabilità di match
simultaneo al posto i e al posto (distinto) j si ha
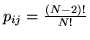 .
Con le notazioni di sopra si osserva che la somma
.
Con le notazioni di sopra si osserva che la somma 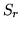 contiene
contiene 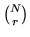 addendi tutti uguali a
addendi tutti uguali a
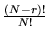 ; pertanto
; pertanto
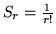 e quindi
e quindi
3. Esercizio.
Un'urna contiene  palline distinguibili, si estrae con rimpiazzo fino a che il
campione ottenuto contenga due elementi uguali; calcolare la probabilità
palline distinguibili, si estrae con rimpiazzo fino a che il
campione ottenuto contenga due elementi uguali; calcolare la probabilità
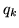 che a questo scopo siano necessarie esattamente
che a questo scopo siano necessarie esattamente  estrazioni.
estrazioni.
Soluzione.
Si osservi che
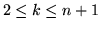 . Siccome si rimpiazza, con
. Siccome si rimpiazza, con  estrazioni si
ottengono
estrazioni si
ottengono 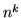 campioni distinti; per ottenere un campione come desiderato, la prima
pallina si può scegliere in
campioni distinti; per ottenere un campione come desiderato, la prima
pallina si può scegliere in  modi, la seconda in
modi, la seconda in 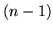 modi,.., la
modi,.., la
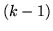 -ma in
-ma in 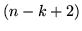 modi e la
modi e la  -ma in
-ma in 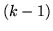 modi. Pertanto:
modi. Pertanto:
4. Formula di Stirling.
La formula di Stirling asserisce l'esistenza di un
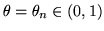 tale che:
tale che:
Nella pratica è sufficiente l'approssimazione
verifichiamo in parte la formula con i calcoli che seguono:
da cui sommando  da 1 a
da 1 a  si ottiene:
si ottiene:
5. Esercizio.
Un'urna contiene 42 palline segnate con le lettere dell'alfabeto italiano: due per
ogni lettera. Si estraggono a caso 21 palline. Calcolare:
i) la probabilità che nel campione compaia una data lettera.
ii)la probabilità che nel campione compaiano tutte le lettere.
iii) la probabilità che si possa formare la parola ``CASSA".
Soluzione.
i). Ci sono
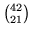 modi di scegliere un campione di 21 lettere, di questi
modi di scegliere un campione di 21 lettere, di questi
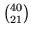 non contengono una data lettera, pertanto la la probabilità
richiesta vale
non contengono una data lettera, pertanto la la probabilità
richiesta vale
ii). Per ogni lettera ci sono due scelte per cui ci sono 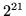 modi di scegliere
un campione che contenga le 21 lettere distinte, pertanto la la probabilità
richiesta vale
modi di scegliere
un campione che contenga le 21 lettere distinte, pertanto la la probabilità
richiesta vale
dove per l'approssimazione abbiamo usato la formula di Stirling.
iii). Distinguiamo per comodità con C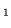 e C
e C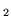 le due lettere ``C" che sono
nell'urna, ci sono
le due lettere ``C" che sono
nell'urna, ci sono
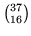 campioni che contengono le lettere C
campioni che contengono le lettere C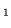 A S S
A, pertanto la la probabilità richiesta vale
A S S
A, pertanto la la probabilità richiesta vale
6. Esercizio.
In una metropoli scegliendo a caso un ristorante si hanno le seguenti
probabilità:
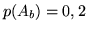 dove
dove 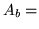 ``si mangia bene"
``si mangia bene"
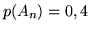 dove
dove 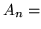 ``si mangia normale"
``si mangia normale"
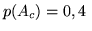 dove
dove 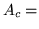 ``si mangia male"
``si mangia male"
Si hanno poi gli eventi
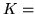 ``caro",
``caro", 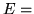 ``equo",
``equo", 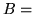 ``buon mercato",
``buon mercato",
e le probabilità condizionali
Calcolare 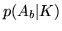 . Se poi sono date le probabilità condizionali
. Se poi sono date le probabilità condizionali
descrivere completamente lo spazio dei campioni.
Soluzione.
Per la formula di Bayes si ha
dove il denominatore della frazione vale 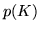 . Si ha
. Si ha
Coi dati ulteriori possiamo calcolare 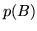 :
:
di conseguenza si ha pure che 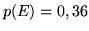 . Consideriamo il quadro
. Consideriamo il quadro
| |
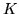 |
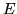 |
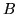 |
Tot |
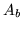 |
|
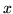 |
|
0,2 |
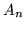 |
|
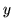 |
|
0,4 |
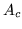 |
|
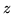 |
|
0,4 |
| Tot |
0,34 |
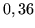 |
0,30 |
1 |
che possiamo completare coi seguenti calcoli:
Possiamo riscrivere il quadro
| |
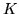 |
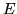 |
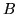 |
Tot |
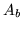 |
0,14 |
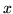 |
0,02 |
0,2 |
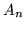 |
0,12 |
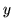 |
0,12 |
0,4 |
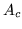 |
0,08 |
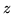 |
0,16 |
0,4 |
| Tot |
0,34 |
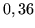 |
0,30 |
1 |
Otteniamo dunque i dati mancanti:



Next: Variabili aleatorie.
Up: Lo spazio di probabilità.
Previous: Probabilità condizionale, indipendenza.
Stefani Gianna
2000-11-06