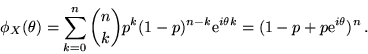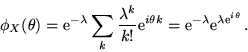Next: Convergenza in legge e
Up: La probabilità nel continuo
Previous: Esercizi e complementi
Date la var.al. 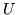 e
e 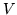 , diremo che
, diremo che 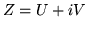 è una var.al. complessa.
Diremo che
è una var.al. complessa.
Diremo che 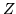 ha media finita se e solo se
ha media finita se e solo se 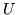 e
e 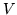 hanno media finita e porremo
hanno media finita e porremo
![$E[Z] = E[U] +i E[V]$](img940.gif) . Si verifica che
. Si verifica che
![$\vert E[Z]\vert \leq E[\vert Z\vert]$](img941.gif) .
.
Sia  una var.al. (reale), si chiama funzione caratteristica di
una var.al. (reale), si chiama funzione caratteristica di  la
funzione a valori complessi
la
funzione a valori complessi 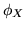 definita su
definita su 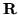 da:
da:
Conviene osservare che
Se  ha densità
ha densità  avremo
avremo
Vale la pena notare che, a meno di una costante, 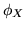 è la trasformata di
Fourier della densità
è la trasformata di
Fourier della densità  .
.
Valgono i seguenti semplici risultati:
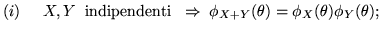
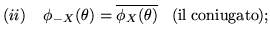
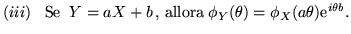
Proviamo per esempio (i) (si tenga conto che dall'ipotesi segue anche
l'indipendenza delle var.al.
 ):
):
Ci domandiamo se una funzione caratteristica 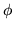 sia derivabile.
La funzione
sia derivabile.
La funzione
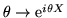 è analitica qualunque valore prenda
è analitica qualunque valore prenda
 ; se l'operazione di derivazione e quella di prendere la media
; se l'operazione di derivazione e quella di prendere la media 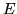 (che è una
integrazione) si possono scambiare, allora
(che è una
integrazione) si possono scambiare, allora 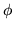 risulta derivabile e le sue
derivate si calcolano subito. Vale il seguente
risulta derivabile e le sue
derivate si calcolano subito. Vale il seguente
Teorema. Qualunque sia
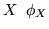 è continua. Se
è continua. Se  ha momento
di ordine
ha momento
di ordine  , allora
, allora 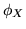 è
è  volte derivabile e si ha
volte derivabile e si ha
Viceversa se 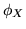 è
è  volte derivabile e
volte derivabile e  è pari, allora
è pari, allora  ha
momento di ordine
ha
momento di ordine  .
.
Si noti in particolare che
questa formula permette di calcolare i momenti.
E' importante sapere che se  e
e 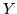 hanno la stessa funzione caratteristica, allora
hanno la stessa densità. Non solo questo è vero, ma si ha pure una formula
esplicita per la densità di
hanno la stessa funzione caratteristica, allora
hanno la stessa densità. Non solo questo è vero, ma si ha pure una formula
esplicita per la densità di  in termini della sua funzione caratteristica:
in termini della sua funzione caratteristica:
Teorema (Formula di inversione). Se 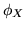 è
sommabile, allora
è
sommabile, allora  è a.c. e per la sua densità
è a.c. e per la sua densità 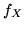 si ha
si ha
Diamo ora degli esempi.
1. Densità esponenziale.
2. Densità normale.
Con una integrazione per parti si trova
da cui, tenendo conto che 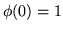 , si ricava
, si ricava
Se
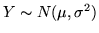 sappiamo che si ha
sappiamo che si ha
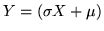 con
con 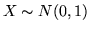 , pertanto applicando la (iii) si ottiene
, pertanto applicando la (iii) si ottiene
Applichiamo questo risultato e (i) alla somma di var.al. normali.
Per 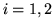 siano
siano
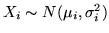 e indipendenti; avremo
e indipendenti; avremo
dove
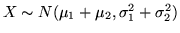 . L'uguaglianza delle funzioni
caratteristiche ci porta a concludere che la somma
. L'uguaglianza delle funzioni
caratteristiche ci porta a concludere che la somma 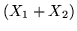 è una var.al.
è una var.al.
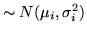 , come avevamo già enunciato.
, come avevamo già enunciato.
1. Densità discrete.
Le funzioni caratteristiche si definiscono anche per va.al. discrete: se  prende
i valori
prende
i valori 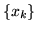 con densità
con densità  si pone
si pone
Diamo in particolare tre esempi.
1. 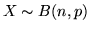 :
:
2.  geometrica:
geometrica:
3.  Poisson di parametro
Poisson di parametro 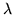 :
:



Next: Convergenza in legge e
Up: La probabilità nel continuo
Previous: Esercizi e complementi
Stefani Gianna
2000-11-06
![]() sia derivabile.
La funzione
sia derivabile.
La funzione
![]() è analitica qualunque valore prenda
è analitica qualunque valore prenda
![]() ; se l'operazione di derivazione e quella di prendere la media
; se l'operazione di derivazione e quella di prendere la media ![]() (che è una
integrazione) si possono scambiare, allora
(che è una
integrazione) si possono scambiare, allora ![]() risulta derivabile e le sue
derivate si calcolano subito. Vale il seguente
risulta derivabile e le sue
derivate si calcolano subito. Vale il seguente ![]() è continua. Se
è continua. Se ![]() ha momento
di ordine
ha momento
di ordine ![]() , allora
, allora ![]() è
è ![]() volte derivabile e si ha
volte derivabile e si ha
![]() e
e ![]() hanno la stessa funzione caratteristica, allora
hanno la stessa densità. Non solo questo è vero, ma si ha pure una formula
esplicita per la densità di
hanno la stessa funzione caratteristica, allora
hanno la stessa densità. Non solo questo è vero, ma si ha pure una formula
esplicita per la densità di ![]() in termini della sua funzione caratteristica:
in termini della sua funzione caratteristica:
![]() è
sommabile, allora
è
sommabile, allora ![]() è a.c. e per la sua densità
è a.c. e per la sua densità ![]() si ha
si ha