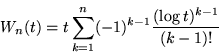Next: Funzioni caratteristiche
Up: La probabilità nel continuo
Previous: Numeri a caso, simulazione
1. Esercizio.
Siano 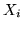 var.al. indipendenti con funzioni di ripartizione
var.al. indipendenti con funzioni di ripartizione
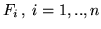 .
Determinare le funzioni di ripartizione di
.
Determinare le funzioni di ripartizione di
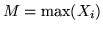 e di
e di
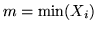 .
.
Soluzione.
2. Esercizio.
Siano 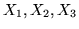 tre var.al. indipendenti uniformemente distribuite in [0,1],
calcolare
tre var.al. indipendenti uniformemente distribuite in [0,1],
calcolare ![$E[Z]$](img342.gif) dove
dove 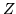 è la var.al. ``valore intermedio delle
è la var.al. ``valore intermedio delle 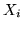 ".
".
Soluzione.
Siano
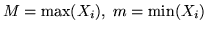 , avremo la rappresentazione
, avremo la rappresentazione
e pertanto
Per le funzioni di ripartizione del massimo e del minimo (tenendo presente
l'indipendenza) si ha:
da cui si ha facilmente
![$E[M] = 3/4, \; E[m] = 1/4$](img904.gif) . Si trova quindi
. Si trova quindi ![$E[Z] = 1/2$](img905.gif) .
.
Naturalmente si può risolvere l'esercizio, con calcoli un po' più
lunghi, determinando la densità di  . Per fare questo poniamo:
. Per fare questo poniamo:
Si osservi ora che
Pertanto la densità vale
e si ritrova che ![$E[Z] = 1/2$](img905.gif) .
.
3. Esercizio.
Siano
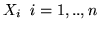 var.al. indipendenti uniformemente distribuite
in [0,1]. Dimostrare che per la funzione di ripartizione del loro prodotto
var.al. indipendenti uniformemente distribuite
in [0,1]. Dimostrare che per la funzione di ripartizione del loro prodotto 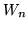 si
ha:
si
ha:
Soluzione.
Verifichiamo la formula per 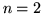 e poi useremo l'induzione. Si ha
e poi useremo l'induzione. Si ha
di conseguenza si ha
Osserviamo ora che
di conseguenza si ha
Si verifica ora facilmente che
da cui si ricava, come si voleva, che
4. Esercizio.
Si prendano tre numeri a caso (in [0,1]), detti 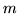 e
e 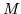 il minimo e il massimo dei
tre, per ogni
il minimo e il massimo dei
tre, per ogni ![$a \in [0,1]$](img922.gif) si calcoli
si calcoli
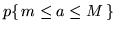
Soluzione.
Risolveremo l'esercizio usando la densità condizionale:
sia 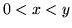 e
e 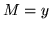 ; calcoliamo la probabilità condizionale
; calcoliamo la probabilità condizionale
Si ha
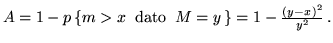 La derivata (rispetto a
La derivata (rispetto a 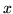 ) di questa ultima è la densità
condizionale, cioè
) di questa ultima è la densità
condizionale, cioè
Per la densità congiunta  del vettore aleatorio
del vettore aleatorio 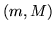 si ha la formula
si ha la formula
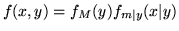 , siccome
, siccome
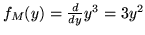 , si
ottiene
, si
ottiene
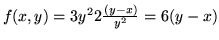 . Se
. Se 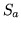 è il
rettangolo
è il
rettangolo
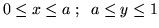 , allora per la probabilità
richiesta P si ha
, allora per la probabilità
richiesta P si ha
Questo esercizio si risolve in modo più semplice come segue:
sia 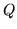 è l'evento
è l'evento
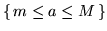 , allora l'evento complementare
, allora l'evento complementare
è unione di due eventi disgiunti, per cui



Next: Funzioni caratteristiche
Up: La probabilità nel continuo
Previous: Numeri a caso, simulazione
Stefani Gianna
2000-11-06