


Next: Esercizi e complementi
Up: La probabilità nel continuo
Previous: Esempi
Consideriamo il seguente problema: è data una var.al.  con legge uniforme su
[0,1] (per esempio ``numeri a caso" generati da un calcolatore) ed è assegnata
una densità
con legge uniforme su
[0,1] (per esempio ``numeri a caso" generati da un calcolatore) ed è assegnata
una densità 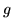 ; si cerca una funzione
; si cerca una funzione 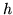 tale che la var.al.
tale che la var.al. 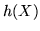 abbia
come densità proprio la
abbia
come densità proprio la 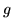 .
.
Supporremo 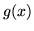 nulla per
nulla per
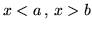 e strettamente positiva
nell'intervallo
e strettamente positiva
nell'intervallo 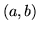 . In queste ipotesi la sua f.r.
. In queste ipotesi la sua f.r. 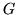 è strettamente crescente e quindi invertibile
nell'intervallo
è strettamente crescente e quindi invertibile
nell'intervallo 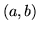 . Sia dunque
. Sia dunque 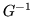 l'inversa di
l'inversa di 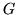 in
in 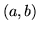 e sia
e sia
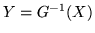 ; avremo (ricordando che la f.r. di
; avremo (ricordando che la f.r. di  è l'identità in [0,1])
è l'identità in [0,1])
Dunque 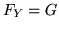 e
e 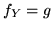 . Facciamo ora degli esempi di simulazioni.
. Facciamo ora degli esempi di simulazioni.
1 Legge esponenziale. La f.r. 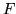 , che è concentrata sulla semiretta
positiva, vale
, che è concentrata sulla semiretta
positiva, vale
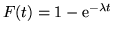 . Si ha
. Si ha
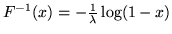 . Se la var.al
. Se la var.al  è uniforme su [0,1], allora la
var.al.
è uniforme su [0,1], allora la
var.al.
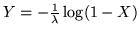 è esponenziale di parametro
è esponenziale di parametro
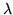 .
.
2 Simulazione prove di Bernoulli. Sia assegnato un numero 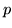 con
con 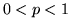 e, per
e, per 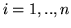 , sia
, sia 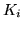 un numero a caso in [0,1]. Definiamo le var.al.
un numero a caso in [0,1]. Definiamo le var.al.
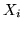 ponendo
ponendo 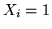 se
se 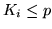 e
e 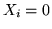 altrimenti. La somma
altrimenti. La somma
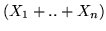 è una var.al.
è una var.al. 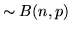 .
.
3 Legge normale. Prendiamo una var.al.  uniforme sul cerchio
unitario e consideriamo, vedi l'esempio 4.6.1, la var.al
uniforme sul cerchio
unitario e consideriamo, vedi l'esempio 4.6.1, la var.al
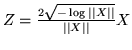 che ha densità
che ha densità
Questo significa che le componenti 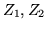 di
di 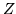 sono indipendenti e
sono indipendenti e
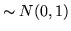 .
.



Next: Esercizi e complementi
Up: La probabilità nel continuo
Previous: Esempi
Stefani Gianna
2000-11-06
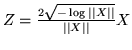 che ha densità
che ha densità