


Next: Numeri a caso, simulazione
Up: La probabilità nel continuo
Previous: Media, momenti e varianza
1 Legge uniforme. Sia la var.al.  uniforme su [0,1]. Allora
uniforme su [0,1]. Allora
2 Leggi normali. Sia 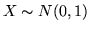 . La
sua densità vale
. La
sua densità vale
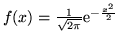 . Siccome
. Siccome 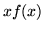 è una funzione dispari su
è una funzione dispari su
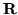 , avremo
, avremo ![$ E[X] = 0$](img316.gif) . In questo caso
. In questo caso
![${\rm Var}(X) = E[X^2]$](img859.gif) ; l'integrale
si calcola per parti e vale 1. Riassumendo
; l'integrale
si calcola per parti e vale 1. Riassumendo
Se
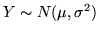 (
(
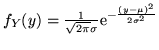 ), allora si
può considerare che
), allora si
può considerare che
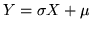 . Si ottiene subito che
. Si ottiene subito che
3 Leggi gamma. Se
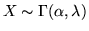 e
e 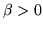 ,
allora con facili calcoli si vede che
,
allora con facili calcoli si vede che
Otteniamo quindi subito
Per le leggi esponenziali (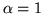 ) si ha
) si ha
Se
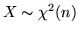 (
(
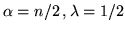 ) si ha
) si ha
Stefani Gianna
2000-11-06
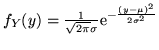 ), allora si
può considerare che
), allora si
può considerare che