


Next: Esempi
Up: La probabilità nel continuo
Previous: Leggi gamma
Definizioni e risultati sono del tutto simili al caso discreto (2.5, 2.6).
Sia  una var.al. continua con densità
una var.al. continua con densità 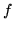 , si dice che
, si dice che  ha media finita
se
ha media finita
se
in tal caso la sua media ![$E[X]$](img422.gif) vale
vale
Teorema 4.9.1. Siano 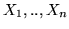 var.al. di densità congiunta
var.al. di densità congiunta 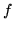 ;
sia
;
sia
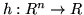 una funzione "ragionevole". Allora la var.al.
una funzione "ragionevole". Allora la var.al.
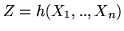 ha media finita se e solo se
ha media finita se e solo se
in tal caso la media ![$E[Z]$](img342.gif) vale
vale
Ecco alcune proprietà della media.
Teorema 4.9.2. Siano  e
e 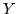 var.al. con media finita. Allora:
var.al. con media finita. Allora:
i) 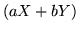 ha media finita e
ha media finita e
![$E[aX + bY] = aE[X]+bE[Y];$](img346.gif)
ii) 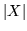 ha media finita e
ha media finita e
![$\vert E[X]\vert \leq E[\vert X\vert];$](img348.gif)
se inoltre  e
e 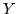 sono indipendenti
sono indipendenti
iii) 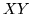 ha media finita e
ha media finita e
![$E[XY] = E[X]E[Y]$](img350.gif) .
.
Sia  una var.al. di densità
una var.al. di densità 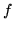 ; diremo che
; diremo che  ha momento di
ordine
ha momento di
ordine 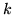 finito (
finito (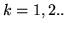 ) se
) se 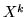 ha media finita. In questo caso
ha media finita. In questo caso
![$E[X^k]$](img359.gif) si chiama momento di ordine
si chiama momento di ordine 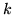 della var.al.
della var.al.  :
:
Se ![$(X-E[X])^k$](img360.gif) ha media finita diremo che
ha media finita diremo che  ha momento centrato di
ordine
ha momento centrato di
ordine 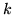 finito e chiameremo
finito e chiameremo ![$E[(X-E[X])^k]$](img361.gif) momento centrato di
ordine
momento centrato di
ordine 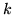 di
di  .
.
Teorema 4.9.3. i) Se  ha momento finito di ordine
ha momento finito di ordine 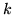 , allora ha
anche momento finito di ordine
, allora ha
anche momento finito di ordine 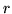 per ogni
per ogni 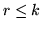 .
.
ii) Se  e
e 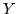 hanno momento finito di ordine
hanno momento finito di ordine 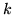 , allora anche
, allora anche 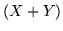 ha momento finito di ordine
ha momento finito di ordine 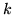 . In particolare se
. In particolare se  ha momento finito di
ordine
ha momento finito di
ordine 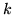 , allora ha anche momento centrato finito di ordine
, allora ha anche momento centrato finito di ordine 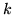 .
.
Ricordiamo che il momento centrato di ordine 2 viene
chiamato varianza:
Vale la disuguaglianza di Chebyshev. Se per la var.al.  esiste il momento
esiste il momento ![$E[X^2]$](img370.gif) (e di conseguenza la varianza) si ha:
(e di conseguenza la varianza) si ha:
in particolare, posto ![$\mu = E[X]$](img373.gif) ,
,
Fissata la var.al.  , denotiamo al solito media e varianza con
, denotiamo al solito media e varianza con
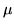 e
e 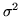 .
.
Se  e
e 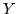 hanno varianza finita, è finita anche la covarianza di
hanno varianza finita, è finita anche la covarianza di  e
e
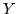 :
:
Teorema 4.9.3. Si ha:
i)
![${\rm Var}(X) = E[X^2] - E[X]^2 $](img383.gif) ;
;
ii)
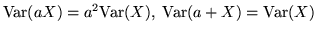 ;
;
iii)
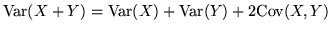 ;
;
iv)
![${\rm Cov}(X,Y) = E[XY] - E[X]E[Y]$](img386.gif) .
.
Se  e
e 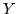 sono indipendenti si ha
sono indipendenti si ha
Quando
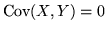 le
var.al.
le
var.al.  e
e 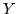 non sono correlate. Per il coefficiente di correlazione
non sono correlate. Per il coefficiente di correlazione
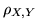 si ha
si ha
Ricordiamo che
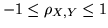 .
.



Next: Esempi
Up: La probabilità nel continuo
Previous: Leggi gamma
Stefani Gianna
2000-11-06