Next: Esempi.
Up: Lo spazio di probabilità.
Previous: Lo spazio di probabilità.
I possibili risultati di un ``esperimento'' costituiscono lo ``spazio
dei campioni" o ``spazio di probabilità''. Le parole chiave sono
spiegate dagli esempi che seguono.
1 Lancio di un dado : {1,2,3,4,5,6}
2 Lancio di una moneta : {T,C}
3 Due lanci successivi di una moneta : {TT,TC,CT,CC}
In questi esempi lo spazio dei campioni ha cardinalità
rispett. 6, 2, 4. Ma ecco un esempio con cardinalità
infinita:
4 Lanci successivi di una moneta finchè venga testa:
Interessa sapere se il risultato dell'esperimento conferma
(rientra in) o no un ``evento'' previsto. Questa nuova parola
chiave sarà spiegata usando gli esempi di sopra.
Sono eventi:
1 : 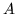 = ``viene un numero pari'' = {2,4,6}
= ``viene un numero pari'' = {2,4,6}
2 : 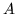 = ``non viene nè testa nè croce'' =
= ``non viene nè testa nè croce'' = 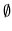
3 : 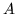 = ``viene almeno una volta testa'' = {TT,TC,CT}
= ``viene almeno una volta testa'' = {TT,TC,CT}
4 : 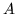 = ``viene testa in non più di 3 lanci'' = {T,CT,CCT}
= ``viene testa in non più di 3 lanci'' = {T,CT,CCT}
Come si vede gli ``eventi'' sono sottoinsiemi
dell'insieme costituito dallo spazio dei campioni, i risultati degli
esperimenti (atomi, eventi semplici) sono dunque gli elementi
(punti) dello spazio dei campioni, che indicheremo con 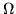 .
Gli eventi sono dunque una sottofamiglia
.
Gli eventi sono dunque una sottofamiglia 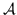 di
di
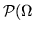 ) (parti di
) (parti di 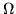 ).
).
Nell'esempio 1 se 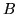 è l'evento ``viene un numero minore o
uguale a 2'' = {1,2}; è naturale considerare come evento
``viene un numero pari oppure viene un numero minore o uguale a 2''
= {1,2,4,6} che poi è
è l'evento ``viene un numero minore o
uguale a 2'' = {1,2}; è naturale considerare come evento
``viene un numero pari oppure viene un numero minore o uguale a 2''
= {1,2,4,6} che poi è 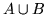 l'evento unione.
l'evento unione.
Nell'esempio 3 è naturale considerare come evento
``non viene mai testa'' = {CC} che poi è
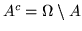 l'evento complementare.
l'evento complementare.
Questa ultima osservazione suggerisce di premettere la
Definizione 1.1.1. Una famiglia 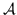 di sottoinsiemi di un
insieme
di sottoinsiemi di un
insieme 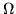 si dice che è una
si dice che è una 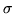 - algebra di
- algebra di 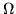 se:
se:
i)
 .
.
ii)
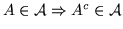 .
.
iii)
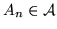 per n = 1,2,...
per n = 1,2,...
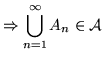 .
.
L'esempio 4 spiega perchè richiedere che l'unione contabile di
eventi sia un evento. Si osservi che dagli assiomi segue che
l'insieme vuoto è un evento così come l'intersezione
contabile di eventi.
Facendo riferimento all'idea intuitiva di probabilità, nei
primi tre esempi concordiamo nel dire che ogni evento semplice
ha la stessa possibilità di realizzarsi: rispett. una su
sei, una su due e una su quattro. Prendiamo ora un dado e segnamo
quattro facce con T e le altre due con C, si ottiene un esempio in
cui lo spazio dei campioni (come insieme) coincide con quello
dell'esempio 2: {T,C}; tuttavia concorderemo nel dire che i
due eventi semplici non hanno la stessa possibilità di
realizzarsi, ne daremo a T quattro su sei e a C due su sei. Se A
non è un evento semplice, concorderemo nell'assegnargli
come possibilità di realizzarsi la somma delle possibilità
degli atomi che lo compongono. Chiamiamo dunque questa
possibilità 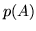 , la probabilità che
, la probabilità che 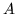 si
verifichi. Siamo indotti subito a dire che
si
verifichi. Siamo indotti subito a dire che 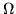 = ``evento
certo" e
= ``evento
certo" e 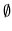 = ``evento impossibile" hanno
probabilità rispett. 1 e 0. Si ha subito da qua che se
= ``evento impossibile" hanno
probabilità rispett. 1 e 0. Si ha subito da qua che se
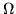 ha cardinalità infinita (come nell'esempio 4),
i suoi atomi non possono avere tutti la stessa
probabilità. (In 4 le probabilità sono rispett.
ha cardinalità infinita (come nell'esempio 4),
i suoi atomi non possono avere tutti la stessa
probabilità. (In 4 le probabilità sono rispett.
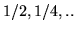 e, come deve essere,
e, come deve essere,
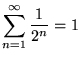 . Si noti che abbiamo tacitamente ammesso
questo fatto: ``prima o poi deve necessariamente uscire testa" che
risulta essere
. Si noti che abbiamo tacitamente ammesso
questo fatto: ``prima o poi deve necessariamente uscire testa" che
risulta essere 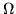 , l'evento certo). La probabilità
, l'evento certo). La probabilità 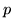 dovrà essere quella che i matematici chiamano una misura
(positiva) definita su una
dovrà essere quella che i matematici chiamano una misura
(positiva) definita su una 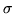 -algebra di un insieme
-algebra di un insieme 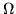 con la condizione che la misura di
con la condizione che la misura di 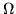 sia 1, cioè
sia 1, cioè
Definizione 1.1.2. Siano 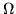 un insieme e
un insieme e 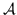 una
una
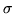 -algebra di
-algebra di 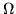 ; una probabilità
; una probabilità 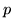 è una
applicazione
è una
applicazione
![$p :{\cal A} \rightarrow [0,1]$](img19.gif) tale che:
tale che:
i) 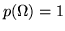 .
.
ii) Se per
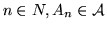 e gli insiemi
e gli insiemi 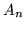 sono
a due a due disgiunti allora (
sono
a due a due disgiunti allora (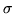 -additività)
-additività)
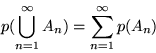
Dall'esempio 4 comprendiamo la necessità di richiedere la
completa additività della probabilità. Siamo ora pronti a
dare la
Definizione 1.1.3. Uno spazio di probabilità
è una terna
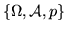 dove
dove 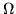 è
un insieme, A una
è
un insieme, A una 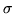 -algebra di
-algebra di
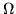 e
e 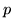 una probabilità su A.
una probabilità su A.
Teorema 1.1.1.
inoltre se 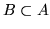 si ha
si ha
Dimostrazione. Basta osservare che
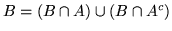 , per cui
, per cui
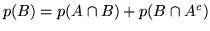 ;
;
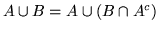 ,
per cui
,
per cui
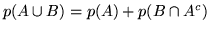 .
.
Nel caso che 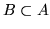 le altre formule si provano scrivendo
le altre formule si provano scrivendo
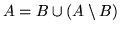 .
.
Si osservi che questo risultato implica in particolare che per eventi qualsiasi
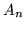 (non necessariamente disgiunti) si ha
(non necessariamente disgiunti) si ha
Per fare un esempio prendiamo il lancio di due dadi. Come spazio dei
campioni si può prendere
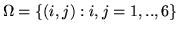 , dove
nella coppia ordinata il primo (secondo) elemento è il numero
uscito nel primo (secondo) dado. Assegnamo la probabilità uniforme,
per cui se
, dove
nella coppia ordinata il primo (secondo) elemento è il numero
uscito nel primo (secondo) dado. Assegnamo la probabilità uniforme,
per cui se
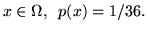 Calcoliamo la
probabilità dell'evento
Calcoliamo la
probabilità dell'evento 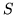 = ``esce almeno una volta il 6". Le
coppie che non contengono il 6 sono 25, per cui
= ``esce almeno una volta il 6". Le
coppie che non contengono il 6 sono 25, per cui
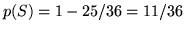 . Si poteva usare il Teorema di sopra:
. Si poteva usare il Teorema di sopra:
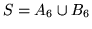 dove
dove
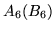 è l'insieme delle coppie con primo (secondo) elemento
il 6. Si ha
è l'insieme delle coppie con primo (secondo) elemento
il 6. Si ha
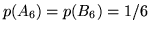 ; inoltre si ha
; inoltre si ha
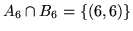 , per cui
, per cui
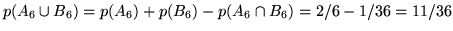 .
.
Teorema 1.1.2. Sia
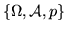 uno spazio di probabilità: se
uno spazio di probabilità: se 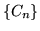 è
una successione crescente di elementi di
è
una successione crescente di elementi di 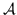 allora
allora
se 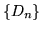 è una successione decrescente di elementi di
è una successione decrescente di elementi di
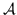 allora
allora
Dimostrazione. Poniamo
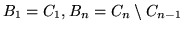 , allora i
, allora i 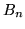 sono in
sono in 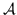 ,
sono a due a due disgiunti e inoltre
,
sono a due a due disgiunti e inoltre
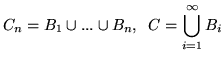 . Pertanto
. Pertanto
e la prima formula segue dalla definizione di
somma di una serie.
Poniamo ora
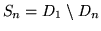 , allora gli
, allora gli 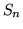 sono
una successione crescente e
sono
una successione crescente e
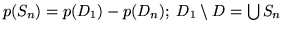 , applicando
la formula precedente si ha
, applicando
la formula precedente si ha
e questo prova la seconda formula.
Come applicazione di questa seconda formula dimostriamo l'utile
Teorema 1.1.3 (Lemma di Cantelli). Sia 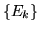 una
successione di eventi tale che
una
successione di eventi tale che
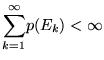 ; allora la probabilità che si verifichino
simultaneamente infiniti eventi della successione è nulla.
; allora la probabilità che si verifichino
simultaneamente infiniti eventi della successione è nulla.
Dimostrazione. Sia 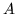 l'evento ``si verificano simultaneamente
infiniti eventi
l'evento ``si verificano simultaneamente
infiniti eventi 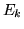 " e poniamo
" e poniamo
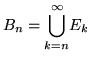 . Sia
. Sia 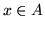 , se
, se 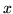 non appartenesse a un
non appartenesse a un 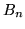 per un certo
per un certo  ,
, 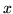 apparterrebbe solo a un numero finito di
apparterrebbe solo a un numero finito di 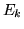 , pertanto
, pertanto
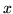 sta in ogni
sta in ogni 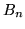 e quindi
e quindi
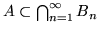 .
Sia ora
.
Sia ora
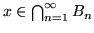 , Se
, Se 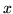 appartenesse solo a un numero
finito di
appartenesse solo a un numero
finito di 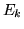 , esisterebbe
, esisterebbe 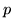 tale che
tale che 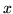 non sta in
non sta in 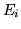 per
per 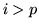 , ma
allora
, ma
allora 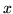 non starebbe in
non starebbe in 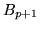 : una contraddizione. Abbiamo provato che
: una contraddizione. Abbiamo provato che
Siccome 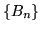 decresce si ha
decresce si ha
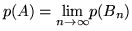 ; d'altra parte si ha
; d'altra parte si ha
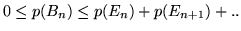 e dal fatto che la serie
e dal fatto che la serie 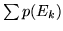 converge segue subito che
converge segue subito che
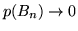 .
.



Next: Esempi.
Up: Lo spazio di probabilità.
Previous: Lo spazio di probabilità.
Stefani Gianna
2000-11-06
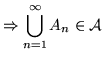 .
.
![]() , la probabilità che
, la probabilità che ![]() si
verifichi. Siamo indotti subito a dire che
si
verifichi. Siamo indotti subito a dire che ![]() = ``evento
certo" e
= ``evento
certo" e ![]() = ``evento impossibile" hanno
probabilità rispett. 1 e 0. Si ha subito da qua che se
= ``evento impossibile" hanno
probabilità rispett. 1 e 0. Si ha subito da qua che se
![]() ha cardinalità infinita (come nell'esempio 4),
i suoi atomi non possono avere tutti la stessa
probabilità. (In 4 le probabilità sono rispett.
ha cardinalità infinita (come nell'esempio 4),
i suoi atomi non possono avere tutti la stessa
probabilità. (In 4 le probabilità sono rispett.
![]() e, come deve essere,
e, come deve essere,
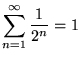 . Si noti che abbiamo tacitamente ammesso
questo fatto: ``prima o poi deve necessariamente uscire testa" che
risulta essere
. Si noti che abbiamo tacitamente ammesso
questo fatto: ``prima o poi deve necessariamente uscire testa" che
risulta essere ![]() , l'evento certo). La probabilità
, l'evento certo). La probabilità ![]() dovrà essere quella che i matematici chiamano una misura
(positiva) definita su una
dovrà essere quella che i matematici chiamano una misura
(positiva) definita su una ![]() -algebra di un insieme
-algebra di un insieme ![]() con la condizione che la misura di
con la condizione che la misura di ![]() sia 1, cioè
sia 1, cioè
![]() un insieme e
un insieme e ![]() una
una
![]() -algebra di
-algebra di ![]() ; una probabilità
; una probabilità ![]() è una
applicazione
è una
applicazione
![]() tale che:
tale che: ![]() .
. ![]() e gli insiemi
e gli insiemi ![]() sono
a due a due disgiunti allora (
sono
a due a due disgiunti allora (![]() -additività)
-additività)
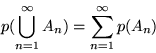
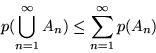
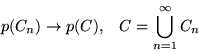
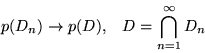
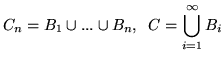 . Pertanto
. Pertanto
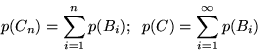
![]() una
successione di eventi tale che
una
successione di eventi tale che
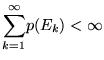 ; allora la probabilità che si verifichino
simultaneamente infiniti eventi della successione è nulla.
; allora la probabilità che si verifichino
simultaneamente infiniti eventi della successione è nulla. ![]() l'evento ``si verificano simultaneamente
infiniti eventi
l'evento ``si verificano simultaneamente
infiniti eventi ![]() " e poniamo
" e poniamo
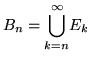 . Sia
. Sia ![]() , se
, se ![]() non appartenesse a un
non appartenesse a un ![]() per un certo
per un certo ![]() ,
, ![]() apparterrebbe solo a un numero finito di
apparterrebbe solo a un numero finito di ![]() , pertanto
, pertanto
![]() sta in ogni
sta in ogni ![]() e quindi
e quindi
![]() .
Sia ora
.
Sia ora
![]() , Se
, Se ![]() appartenesse solo a un numero
finito di
appartenesse solo a un numero
finito di ![]() , esisterebbe
, esisterebbe ![]() tale che
tale che ![]() non sta in
non sta in ![]() per
per ![]() , ma
allora
, ma
allora ![]() non starebbe in
non starebbe in ![]() : una contraddizione. Abbiamo provato che
: una contraddizione. Abbiamo provato che