


Next: Media, momenti e varianza
Up: La probabilità nel continuo
Previous: Leggi normali
Si chiama 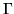 la funzione da
la funzione da 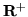 a
a 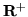 :
:
Con integrazioni per parti si vede che
Se  è un intero positivo allora
è un intero positivo allora
Si dice che una var.al.  segue una legge gamma di parametri
segue una legge gamma di parametri
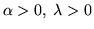 oppure che
oppure che
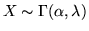 se la sua
densità è concentrata su
se la sua
densità è concentrata su  e vale
e vale
(Non è difficile verificare con un'integrazione che 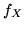 è effettivamente
una densità).
è effettivamente
una densità).
Esempio. Sia
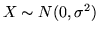 e quindi di
densità
e quindi di
densità
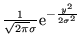 . La
densità
. La
densità 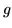 di
di 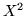 sappiamo calcolarla e vale
sappiamo calcolarla e vale
Poichè 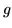 è una densità, si vede che
è una densità, si vede che 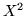 deve essere una
deve essere una
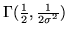 ; si deduce quindi che
per
; si deduce quindi che
per
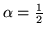 e per
e per
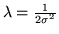 si ha
si ha
cioè l'importante uguaglianza
Teorema 4.8.. Siano  e
e 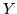 due var.al. indipendenti di legge risp.
due var.al. indipendenti di legge risp.
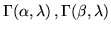 , allora
, allora
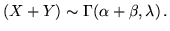
Dimostrazione. Ricordiamo che la formula per la densità della somma
di var.al. indipendenti è
Siccome le 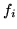 sono nulle per valori negativi della variabile, avremo in
effetti un integrale esteso all'intervallo
sono nulle per valori negativi della variabile, avremo in
effetti un integrale esteso all'intervallo ![$[0,z]$](img829.gif) :
:
facendo ora nell'integrale il cambiamento di variabile 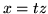 si ottiene
si ottiene
Dunque
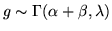 e il termine in
parentesi quadra vale
e il termine in
parentesi quadra vale
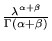 ; si
ha quindi l'importante uguaglianza
; si
ha quindi l'importante uguaglianza
Notiamo due casi particolari:
La legge
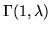 è la legge esponenziale di densità
è la legge esponenziale di densità
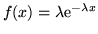 già considerata.
già considerata.
La legge
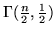 è detta legge del chi quadro
a
è detta legge del chi quadro
a  gradi di libertà e si denota con
gradi di libertà e si denota con 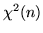 . Nell'esempio precedente
abbiamo visto che se
. Nell'esempio precedente
abbiamo visto che se 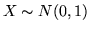 allora
allora
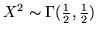 , pertanto se
, pertanto se
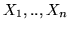 sono var.al. indipendenti
sono var.al. indipendenti 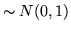 , avremo che
, avremo che
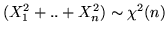 .
.



Next: Media, momenti e varianza
Up: La probabilità nel continuo
Previous: Leggi normali
Stefani Gianna
2000-11-06