


Next: Leggi gamma
Up: La probabilità nel continuo
Previous: Calcolo di leggi
Riprendiamo qui la densità normale 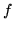 :
:
Sia  una var.al. che abbia per densità questa
una var.al. che abbia per densità questa 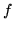 e siano
e siano 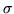 e
e 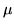 numeri reali con
numeri reali con 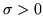 . La var.al.
. La var.al.
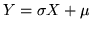 ha, come abbiamo
visto, densità
ha, come abbiamo
visto, densità
Una densità  come sopra si dice normale o gaussiana di
parametri
come sopra si dice normale o gaussiana di
parametri  e
e 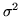 , o anche una
, o anche una
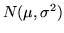 , per la var.al.
, per la var.al. 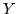 si
usa anche scrivere
si
usa anche scrivere
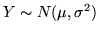 . La
. La 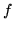 considerata è quindi una
considerata è quindi una
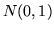 ; una
; una
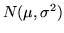 si può riguardare come densità di una var.al.
si può riguardare come densità di una var.al.
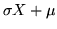 dove
dove
 ha legge
ha legge
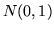 . La f.r.
. La f.r.
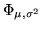 di una
di una
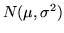 si deduce, come
segue, dalla f.r. di una
si deduce, come
segue, dalla f.r. di una 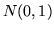 :
:
Faremo vedere, con il metodo delle funzioni caratteristiche, che la somma di 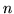 var.al. indipendenti
var.al. indipendenti
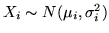 è una
è una
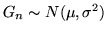 con
con
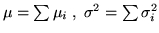 .
.
Stefani Gianna
2000-11-06