


Next: Leggi normali
Up: La probabilità nel continuo
Previous: Densità condizionali
Un problema comune è il seguente: sia  un vettore al.
un vettore al.  -dimensionale di
cui si conosce la densità (congiunta)
-dimensionale di
cui si conosce la densità (congiunta)  e sia
e sia
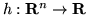 una funzione ``ragionevole": calcolare la densità della var.al.
una funzione ``ragionevole": calcolare la densità della var.al.
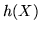 .
.
Una soluzione possibile consiste nel calcolare la f.r. di 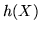 e poi derivarla.
In effetti si ha:
e poi derivarla.
In effetti si ha:
![$F_{h(X)}(t) = p\,\{ h(X) \leq t \,\} =
p\,\{ X \in h^{-1}(-\infty ,t] = A_t \,\} = \int_{A_t} f$](img730.gif) .
.
Esempio. Sia  una var.al. di densità
una var.al. di densità  , calcolare le densità
, calcolare le densità
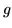 di
di 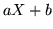 (
(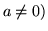 e di
e di 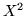 .
.
Nel primo caso, se 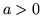 ,
,
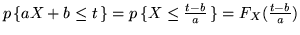 , pertanto derivando si ottiene
, pertanto derivando si ottiene
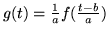 . Se
. Se 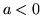 ,
,
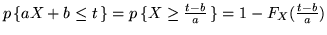 , derivando si ottiene ora
, derivando si ottiene ora
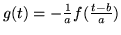 . In definitiva si ha per ogni
. In definitiva si ha per ogni 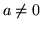 :
:
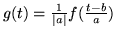 .
.
Indichiamo con 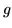 la densità di
la densità di 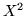 . Si ha, prendendo
. Si ha, prendendo 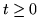 ,
,
e derivando si ottiene
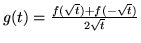 .
.
Teorema. Siano  e
e 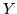 var.al. di densità congiunta
var.al. di densità congiunta  , allora
la densità
, allora
la densità 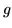 di
di 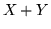 vale
vale
Dimostrazione. Sia
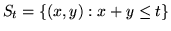 , allora la f.r.
, allora la f.r. 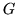 della
somma vale
della
somma vale
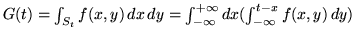 , col cambiamento di
variabile
, col cambiamento di
variabile 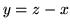 si ottiene
si ottiene
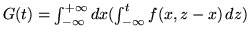 da cui cambiando l'ordine di integrazione si ha
infine
da cui cambiando l'ordine di integrazione si ha
infine
ossia
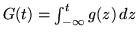 .
.
A volte la densità di una somma si calcola in modo diretto come nel seguente
Esempio. Siano  e
e 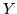 var.al. indipendenti e uniformi in [0,1]. La var.al.
var.al. indipendenti e uniformi in [0,1]. La var.al.
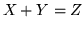 prende valori in [0,2]. Sul quadrato unitario del piano
prende valori in [0,2]. Sul quadrato unitario del piano 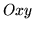 si disegni la
retta di equazione
si disegni la
retta di equazione 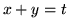 .
. 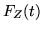 vale l'area della parte di quadrato a sinistra
di questa retta. Conviene distinguere i casi
vale l'area della parte di quadrato a sinistra
di questa retta. Conviene distinguere i casi 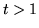 e
e 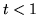 . Avremo
. Avremo
Di conseguenza la densità vale
Nel caso vettoriale per trovare la densità di 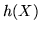 bisogna ricorrere alla
formula del cambiamento di variabili negli integrali multipli.
bisogna ricorrere alla
formula del cambiamento di variabili negli integrali multipli.
Sia
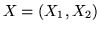 un vettore al. di densità congiunta
un vettore al. di densità congiunta  e sia
e sia
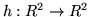 una funzione per cui valga la formula del cambiamento
di variabili negli integrali doppi. Si cerca la densità
una funzione per cui valga la formula del cambiamento
di variabili negli integrali doppi. Si cerca la densità 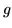 del vettore al.
del vettore al.
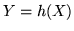 . Abbiamo intanto per un ``ragionevole"
. Abbiamo intanto per un ``ragionevole" 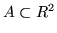 che
che
Applicando il cambiamento di variabile
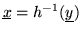 si ha
si ha
dove 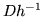 è il determinante jacobiano della trasformazione
è il determinante jacobiano della trasformazione 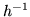 .
.
Siccome per ``quasi tutti" gli 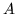 vale l'uguaglianza
vale l'uguaglianza
possiamo concludere che
A volte per studiare un problema conviene cambiare coordinate. Trattiamo il caso
delle coordinate polari sul piano.
Sia 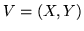 un vettore al. di densità congiunta
un vettore al. di densità congiunta  ; passiamo alle
coordinate polari ponendo
; passiamo alle
coordinate polari ponendo
dove
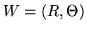 è ristretto a
è ristretto a
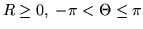 .
Se
.
Se 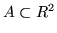 avremo
avremo
dove 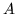 è l'immagine di
è l'immagine di 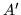 nella trasformazione. Ma gli eventi
nella trasformazione. Ma gli eventi 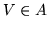 e
e 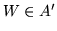 sono identici; questo significa che la densità congiunta
sono identici; questo significa che la densità congiunta 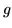 di
di 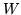 vale
vale
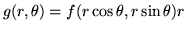 .
.
Applichiamo questo risultato alla densità uniforme sul cerchio già considerata
(vedi Esempio 3 in 4.4.). Avremo
da cui si ottengono con semplici calcoli le densità marginali
Siccome
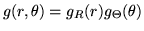 si vede che le var.al.
si vede che le var.al. 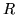 e
e 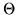 sono indipendenti (mentre
sono indipendenti (mentre  e
e 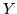 non lo sono).
non lo sono).
Esempio 4.6.1. Sia
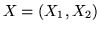 una var.al. uniforme
sul cerchio unitario, si cerca la densità della var.al.
una var.al. uniforme
sul cerchio unitario, si cerca la densità della var.al.
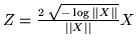 .
.
Passando alle coordinate polari sia
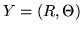 , per quanto visto
, per quanto visto 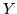 ha densità
ha densità 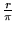 sul rettangolo (del piano
sul rettangolo (del piano 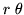 )
)
![$[0,1] \times [-\pi, \pi]$](img788.gif) . Si ha
. Si ha
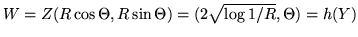 . Indicando con
. Indicando con
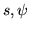 le variabili della inversa, si vede che
le variabili della inversa, si vede che
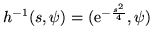 . Il modulo del determinante
Jacobiano della
. Il modulo del determinante
Jacobiano della 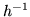 vale
vale
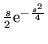 . La
densità di
. La
densità di 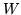 vale pertanto
vale pertanto
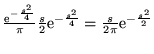 .
Dividendo per
.
Dividendo per 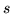 e rimettendo le coordinate cartesiane si ottiene
la densità richiesta di
e rimettendo le coordinate cartesiane si ottiene
la densità richiesta di 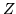 espressa appunto con le coordinate
cartesiane:
espressa appunto con le coordinate
cartesiane:
Poichè 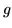 è una densità, deve avere integrale su
è una densità, deve avere integrale su 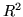 uguale a 1, da questa osservazione si deduce che
uguale a 1, da questa osservazione si deduce che



Next: Leggi normali
Up: La probabilità nel continuo
Previous: Densità condizionali
Stefani Gianna
2000-11-06
![]() bisogna ricorrere alla
formula del cambiamento di variabili negli integrali multipli.
bisogna ricorrere alla
formula del cambiamento di variabili negli integrali multipli.
![]() un vettore al. di densità congiunta
un vettore al. di densità congiunta ![]() e sia
e sia
![]() una funzione per cui valga la formula del cambiamento
di variabili negli integrali doppi. Si cerca la densità
una funzione per cui valga la formula del cambiamento
di variabili negli integrali doppi. Si cerca la densità ![]() del vettore al.
del vettore al.
![]() . Abbiamo intanto per un ``ragionevole"
. Abbiamo intanto per un ``ragionevole" ![]() che
che
![]() un vettore al. di densità congiunta
un vettore al. di densità congiunta ![]() ; passiamo alle
coordinate polari ponendo
; passiamo alle
coordinate polari ponendo
![]() una var.al. uniforme
sul cerchio unitario, si cerca la densità della var.al.
una var.al. uniforme
sul cerchio unitario, si cerca la densità della var.al.
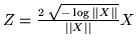 .
.
![]() , per quanto visto
, per quanto visto ![]() ha densità
ha densità ![]() sul rettangolo (del piano
sul rettangolo (del piano ![]() )
)
![]() . Si ha
. Si ha
![]() . Indicando con
. Indicando con
![]() le variabili della inversa, si vede che
le variabili della inversa, si vede che
![]() . Il modulo del determinante
Jacobiano della
. Il modulo del determinante
Jacobiano della ![]() vale
vale
![]() . La
densità di
. La
densità di ![]() vale pertanto
vale pertanto
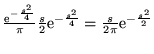 .
Dividendo per
.
Dividendo per ![]() e rimettendo le coordinate cartesiane si ottiene
la densità richiesta di
e rimettendo le coordinate cartesiane si ottiene
la densità richiesta di ![]() espressa appunto con le coordinate
cartesiane:
espressa appunto con le coordinate
cartesiane: