


Next: Calcolo di leggi
Up: La probabilità nel continuo
Previous: Indipendenza
Due var.al,  e
e 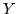 abbiano densità congiunta
abbiano densità congiunta 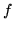 e marginali
e marginali 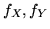 .
Si chiama densità condizionale di
.
Si chiama densità condizionale di  dato
dato 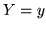 la quantità
la quantità
se 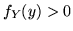 , se
, se 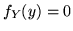 porremo
porremo
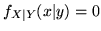 . Si osservi che per
ogni
. Si osservi che per
ogni 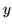 con
con 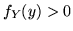 la funzione
la funzione
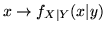 è una
densità, dal momento che
è una
densità, dal momento che
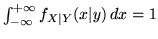 .
Nell'esempio 3 del paragrafo precedente si ha che, se
.
Nell'esempio 3 del paragrafo precedente si ha che, se 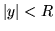 , allora
, allora
quindi la densità condizionale di  dato
dato 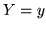 è la densità
uniforme sull'intervallo
è la densità
uniforme sull'intervallo
![$[-\sqrt{R^2-y^2}, \sqrt{R^2-y^2}]$](img727.gif) .
.
Osserviamo che si possono definire densità condizionali anche per vettori al.
misti cioè aventi una componente a.c. e una discreta.
Stefani Gianna
2000-11-06
