


Next: Densità condizionali
Up: La probabilità nel continuo
Previous: Densità congiunte
Due var.al.  e
e 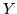 si dicono indipendenti (la definizione si estende a un
numero qualsiasi) se per ogni scelta dei numeri
si dicono indipendenti (la definizione si estende a un
numero qualsiasi) se per ogni scelta dei numeri 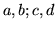 si ha:
si ha:
Se esistono le densità marginali 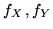 e la densità congiunta
e la densità congiunta
 ,
allora la condizione di indipendenza si traduce nella formula
,
allora la condizione di indipendenza si traduce nella formula
questa uguaglianza è certo verificata se per ogni 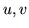 si ha
si ha
Si può provare che quest'ultima condizione è anche necessaria per
l'indipendenza.
Esempio 1. Ago di Buffon. Il piano 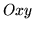 è
diviso con strisce parallele all'asse
è
diviso con strisce parallele all'asse 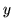 di larghezza unitaria. Un ago di lunghezza
unitaria viene gettato a caso sul piano. Si domanda quanto vale la probabilità che
l'ago stia in due strisce. Consideriamo il centro dell'ago: la sua posizione è
determinata da due coordinate, ma possiamo ignorare la
di larghezza unitaria. Un ago di lunghezza
unitaria viene gettato a caso sul piano. Si domanda quanto vale la probabilità che
l'ago stia in due strisce. Consideriamo il centro dell'ago: la sua posizione è
determinata da due coordinate, ma possiamo ignorare la 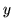 e ridurre la
e ridurre la 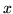 modulo 1
(considerare cioè come se la
modulo 1
(considerare cioè come se la 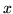 prendesse solo valori in [0,1]). La direzione
dell'ago sia l'angolo che fa l'ago con l'asse
prendesse solo valori in [0,1]). La direzione
dell'ago sia l'angolo che fa l'ago con l'asse 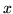 ; una rotazione dell'ago (attorno al
centro) di
; una rotazione dell'ago (attorno al
centro) di
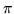 riproduce la sua posizione per cui l'angolo può essere preso variabile tra
riproduce la sua posizione per cui l'angolo può essere preso variabile tra
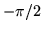 e
e 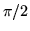 . Indicheremo con
. Indicheremo con  la var.al. ``centro dell'ago" e con
la var.al. ``centro dell'ago" e con 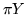 la var.al. ``direzione". Si suppone che
la var.al. ``direzione". Si suppone che  e
e 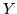 siano indipendenti con densità
uniforme negli intervalli [0,1] e [-1/2, 1/2]. Si ha che l'ago taglia un confine se
e solo se
siano indipendenti con densità
uniforme negli intervalli [0,1] e [-1/2, 1/2]. Si ha che l'ago taglia un confine se
e solo se
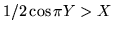 oppure
oppure
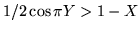 . Nel quadrato
. Nel quadrato
![$[0,1] \times [-1/2, 1/2]$](img696.gif) si disegnino le curve
si disegnino le curve
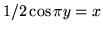 e
e
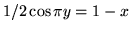 . La probabilità P richiesta è misurata dall'area di
quella parte del quadrato limitata dalle curve e dalle parallele all'asse
. La probabilità P richiesta è misurata dall'area di
quella parte del quadrato limitata dalle curve e dalle parallele all'asse 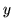 .
Tenendo conto delle simmetrie questa area vale
.
Tenendo conto delle simmetrie questa area vale
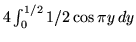 per
cui P = 2/
per
cui P = 2/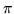 .
.
Esempio 2. Triangoli. Si prendono tre punti a caso nel piano, qual'è
la probabilità P che il triangolo ottenuto sia
ottusangolo? Possiamo ritenere i tre punti distribuiti uniformemente sulla
circonferenza unitaria; due di essi saranno agli estremi di una corda intercettata
da un angolo 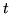 , in tal caso il terzo punto determina un triangolo ottusangolo
quando si trovi nella parte di semicirconferenza determinata da angolo minore o
uguale di
, in tal caso il terzo punto determina un triangolo ottusangolo
quando si trovi nella parte di semicirconferenza determinata da angolo minore o
uguale di 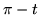 . Tenuto conto delle simmetrie si trova P =
. Tenuto conto delle simmetrie si trova P =
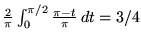 . Senza calcoli si perviene allo
stesso risultato nel modo seguente. Siano
. Senza calcoli si perviene allo
stesso risultato nel modo seguente. Siano 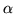 e
e 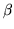 due degli angoli del
triangolo:
due degli angoli del
triangolo:
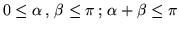 ; si
consideri poi nel piano cartesiano la densità uniforme sul triangolo di vertici
; si
consideri poi nel piano cartesiano la densità uniforme sul triangolo di vertici
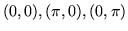 .
.
Esempio 3. Densità uniforme sul cerchio. Nel cerchio 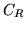 con centro
nell'origine e raggio
con centro
nell'origine e raggio 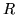 sia data la densità uniforme
sia data la densità uniforme
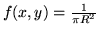 se
se 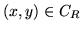 e 0 altrimenti. Vogliamo calcolare le densità
marginali
e 0 altrimenti. Vogliamo calcolare le densità
marginali 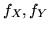 . Sappiamo che
. Sappiamo che
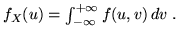 Nel nostro caso: se
Nel nostro caso: se
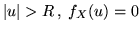 ; se
; se 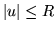 si ha
si ha
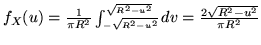 . Analogo risultato si avrà per
. Analogo risultato si avrà per 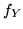 . Si
osservi che le var.al.
. Si
osservi che le var.al.  e
e 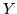 non sono indipendenti. Infatti se
non sono indipendenti. Infatti se 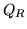 è il
quadrato di lato
è il
quadrato di lato 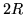 centrato nell'origine, allora se
centrato nell'origine, allora se
Come nel caso discreto vale il seguente risultato:
Se 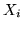 sono vettori al.
indipendenti e
sono vettori al.
indipendenti e 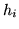 funzioni a valori reali ``ragionevoli'', allora anche
funzioni a valori reali ``ragionevoli'', allora anche 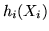 sono indipendenti.
sono indipendenti.



Next: Densità condizionali
Up: La probabilità nel continuo
Previous: Densità congiunte
Stefani Gianna
2000-11-06
![]() sono vettori al.
indipendenti e
sono vettori al.
indipendenti e ![]() funzioni a valori reali ``ragionevoli'', allora anche
funzioni a valori reali ``ragionevoli'', allora anche ![]() sono indipendenti.
sono indipendenti.