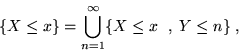Next: Indipendenza
Up: La probabilità nel continuo
Previous: Esempi
Considereremo, per semplicità solo vettori aleatori bidimensionali. Sia 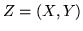 un tale vettore; la f.r.
un tale vettore; la f.r. 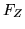 congiunta di
congiunta di 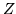 è definita da:
è definita da:
dove
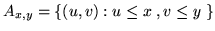 .
.
Diremo che  ha densità congiunta
ha densità congiunta 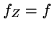 se
se
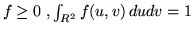 , (cioè
, (cioè 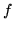 è una
densità) e inoltre
è una
densità) e inoltre
Per sottoinsiemi ``ragionevoli" 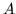 di
di 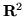 avremo in generale la formula
avremo in generale la formula
Conoscendo f.r. e densità congiunte di un vettore al. 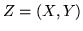 , calcoliamone
f.r. e densità marginali. Si osservi che
, calcoliamone
f.r. e densità marginali. Si osservi che
per cui
e, allo stesso modo
Per calcolare le densità marginali osserviamo che, detta 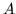 la striscia
la striscia
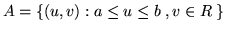 , si ha
, si ha
Posto
otteniamo
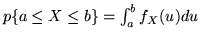 . Questo mostra che
. Questo mostra che
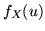 è una densità per
è una densità per  . Analogamente si vede che è una
densità per
. Analogamente si vede che è una
densità per 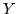 :
:



Next: Indipendenza
Up: La probabilità nel continuo
Previous: Esempi
Stefani Gianna
2000-11-06