


Next: Densità congiunte
Up: La probabilità nel continuo
Previous: Prime definizioni
1. Densità esponenziale. Per ogni 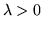 si definisce una f.r.
ponendo
si definisce una f.r.
ponendo
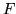 è a.c. ; derivando si ottiene la sua densità
è a.c. ; derivando si ottiene la sua densità
2. Densità uniforme. Definiamo una f.r. ponendo
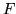 è a.c. ; derivando si ottiene la sua densità
è a.c. ; derivando si ottiene la sua densità
Se  è una var.al. con questa densità uniforme e se
è una var.al. con questa densità uniforme e se
![$A \subset [0,1]$](img662.gif) è
misurabile, allora
è
misurabile, allora
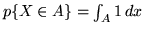 , la misura di Lebesgue di
, la misura di Lebesgue di 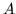 .
.
3. Densità normale. La f.r. (distribuzione) normale 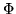 , che abbiamo
intodotto nel capitolo 3, è definita da:
, che abbiamo
intodotto nel capitolo 3, è definita da:
e la sua densità è
La f.r. del primo esempio non è
derivabile nell'origine, quella del secondo non lo è nell'origine e nel punto 1.
Stefani Gianna
2000-11-06