


Next: Esempi
Up: La probabilità nel continuo
Previous: La probabilità nel continuo
Definizione 4.1.1. Una
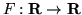 è detta
funzione di ripartizione (f.r.) se gode
delle seguenti proprietà:
è detta
funzione di ripartizione (f.r.) se gode
delle seguenti proprietà:
1) 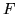 è non decrescente e continua a destra;
è non decrescente e continua a destra;
2)
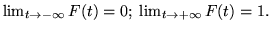
Ricordiamo che per una var.al.  abbiamo già definito
la sua funzione di ripartizione ponendo:
abbiamo già definito
la sua funzione di ripartizione ponendo:
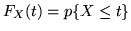 .
Le definizioni sono consistenti: infatti
.
Le definizioni sono consistenti: infatti 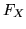 verifica le proprietà 1)
e 2). Proviamo la 1). E' ovvio che
verifica le proprietà 1)
e 2). Proviamo la 1). E' ovvio che 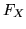 sia non decrescente. Sia
sia non decrescente. Sia 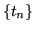 una
successione che tende a
una
successione che tende a 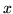 decrescendo, dobbiamo mostrare che
decrescendo, dobbiamo mostrare che
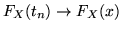 . Sia
. Sia
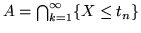 , avendosi una successione
decrescente di eventi, per il Teorema 1.1.2
, avendosi una successione
decrescente di eventi, per il Teorema 1.1.2
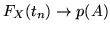 . Resta da
provare che
. Resta da
provare che
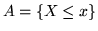 . E' ovvio che
. E' ovvio che
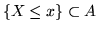 ; se
; se 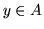 , allora
, allora 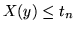 per ogni
per ogni  e pertanto anche
e pertanto anche 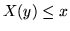 , cioè
, cioè
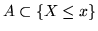 .
In modo simile si prova la 2).
.
In modo simile si prova la 2).
Ogni f.r. 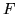 , come si vede subito, soddisfa pure:
, come si vede subito, soddisfa pure:
3)
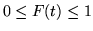 ;
;
4)
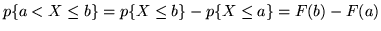 .
.
Come ogni funzione monotona la 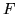 ammette in ogni punto
ammette in ogni punto 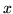 anche il limite
sinistro che si denoterà con
anche il limite
sinistro che si denoterà con 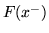 . Avremo dunque sempre
. Avremo dunque sempre
al solito modo si verifica poi che
in particolare
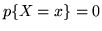 se
se 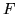 è continua in
è continua in 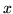 .
.
E' importante sottolineare il fatto che le proprietà 1) e 2) caratterizzano le
f.r.
Definizione 4.1.2. Una
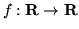 è una
densità se è misurabile (secondo Lebesgue) e
è una
densità se è misurabile (secondo Lebesgue) e
Conviene osservare subito che se 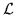 è la
è la 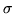 -algebra dei sottoinsiemi
di
-algebra dei sottoinsiemi
di 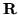 misurabili secondo Lebesgue, avendo a disposizione una densità
misurabili secondo Lebesgue, avendo a disposizione una densità  ,
si ottiene uno spazio di probabilità
,
si ottiene uno spazio di probabilità
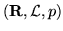 ponendo, per
ponendo, per
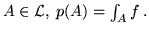
Sempre essendo  una densità,
se poniamo
una densità,
se poniamo
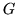 risulta una f.r. con la proprietà ulteriore di essere assolutamente
continua (vedi appendice), inoltre
risulta una f.r. con la proprietà ulteriore di essere assolutamente
continua (vedi appendice), inoltre 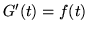 quasi ovunque (q.o.) cioè tranne
al più un insieme di misura (di Lebesgue) nulla.
quasi ovunque (q.o.) cioè tranne
al più un insieme di misura (di Lebesgue) nulla.
L'assoluta continuità è una proprietà più forte della
continuità. In generale se 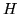 è una funzione assolutamente continua
(a.c.)
è una funzione assolutamente continua
(a.c.) 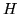 è (derivabile q.o. ed è) primitiva della sua derivata, cioè
è (derivabile q.o. ed è) primitiva della sua derivata, cioè
Se 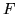 è una f.r. e
è una f.r. e  una densità, diremo che
una densità, diremo che 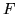 ammette
ammette  come
densità se
come
densità se
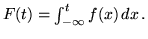 Se una f.r.
Se una f.r. 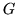 è
a.c. allora ammette come densità la sua derivata
è
a.c. allora ammette come densità la sua derivata 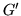 .
Esistono tuttavia f.r.
.
Esistono tuttavia f.r. 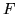 continue che non ammettono densità.(Questo nonostante
che ogni f.r., essendo monotona, sia derivabile q.o.).
continue che non ammettono densità.(Questo nonostante
che ogni f.r., essendo monotona, sia derivabile q.o.).
Definizione 4.1.3. Diremo che una var.al.  è a.c. se la
sua f.r.
è a.c. se la
sua f.r. 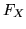 ammette densità (ed è quindi a.c.).
ammette densità (ed è quindi a.c.).
Sia  a.c. con f.r.
a.c. con f.r. 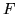 e densità
e densità  , allora si ha
, allora si ha
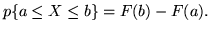 Più in generale se
Più in generale se 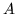 e misurabile in
e misurabile in 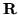 si ha
si ha



Next: Esempi
Up: La probabilità nel continuo
Previous: La probabilità nel continuo
Stefani Gianna
2000-11-06