


Next: Esercizi e complementi
Up: La legge dei grandi
Previous: La legge debole
Cominciamo coll' enunciare una disuguaglianza che è più fine di quella di
Chebyshev. (Dimostrazione in appendice).
Teorema 3.2.1 (Disuguaglianza di Kolmogorov).
Siano
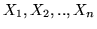 var.al. indipendenti aventi media
var.al. indipendenti aventi media 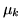 e varianza
e varianza
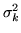 e sia
e sia
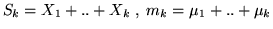 . Dato
. Dato 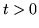 consideriamo le
consideriamo le  disuguaglianze
disuguaglianze
Sia 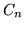 l'evento ``si verifica almeno una delle disuguaglianze (*)"; allora
l'evento ``si verifica almeno una delle disuguaglianze (*)"; allora
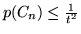 .
.
Si osservi che per 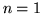 la disuguaglianza di Kolmogorov si riduce alla
disuguaglianza di Chebyshev. In effetti basta prendere
la disuguaglianza di Kolmogorov si riduce alla
disuguaglianza di Chebyshev. In effetti basta prendere
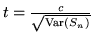
Se le var.al. hanno la stessa media 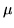 e la stessa varianza
e la stessa varianza 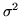 , allora
con la scelta di
, allora
con la scelta di
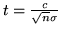 in luogo delle
in luogo delle  disuguaglianze
(*) si hanno le
disuguaglianze
(*) si hanno le  disuguaglianze
disuguaglianze
Per illustrare il significato (e i limiti) della legge debole e per introdurrre la
legge forte consideriamo per semplicità lo schema di Bernoulli 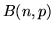 .
Indichiamo con
.
Indichiamo con 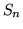 il numero di successi nelle
il numero di successi nelle  prove. La nozione intuitiva di
probabilità vorrebbe che per la frequenza di successi
prove. La nozione intuitiva di
probabilità vorrebbe che per la frequenza di successi 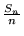 si avesse
si avesse
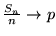 : in effetti questo evento si verifica con
probabilità 1, ma la questione andrebbe trattata con la probabilità nel
continuo. Comunque questo risultato non è contenuto nella legge debole (ma
in quella forte). La legge debole afferma che
: in effetti questo evento si verifica con
probabilità 1, ma la questione andrebbe trattata con la probabilità nel
continuo. Comunque questo risultato non è contenuto nella legge debole (ma
in quella forte). La legge debole afferma che
Questa formula ci dice che, per  fissato sufficientemente grande, la frequenza di
successi
fissato sufficientemente grande, la frequenza di
successi 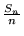 ha una buona probabilità di essere vicina a
ha una buona probabilità di essere vicina a 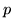 ; ma non
ci dice che tale frequenza sia vincolata a rimanere vicino a
; ma non
ci dice che tale frequenza sia vincolata a rimanere vicino a 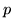 .
Per esempio viene lasciata aperta la possibilità che
per infiniti
.
Per esempio viene lasciata aperta la possibilità che
per infiniti 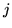 si verifichi l'evento
si verifichi l'evento
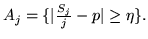 In effetti non è
così: faremo
ora vedere che con probabilità 1,
In effetti non è
così: faremo
ora vedere che con probabilità 1,
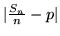 diventa e resta
piccolo.
diventa e resta
piccolo.
Schema di Bernoulli: (legge forte dei grandi numeri).
Per ogni 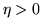 è nulla la probabilità che si verifichino
simultaneamente infiniti eventi
è nulla la probabilità che si verifichino
simultaneamente infiniti eventi
Dimostrazione. Per il lemma di Cantelli (Teorema 1.1.3) basta dimostrare che
la serie 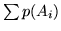 converge. Indichiamo con
converge. Indichiamo con 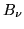 l'evento: ``per almeno un
l'evento: ``per almeno un
 , con
, con
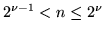 , vale la diseguaglianza
, vale la diseguaglianza
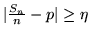 ". Basterà provare che la serie
". Basterà provare che la serie
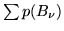 converge. Il verificarsi di
converge. Il verificarsi di 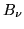 implica che
implica che
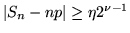 . Applichiamo ora la disuguaglianza di
Kolmogorov: (abbiamo qui
. Applichiamo ora la disuguaglianza di
Kolmogorov: (abbiamo qui
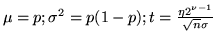 ) si avrà
) si avrà
e questo prova che la serie converge.
Enunciamo dunque il
Teorema 3.2.2 (Legge forte dei grandi numeri). Sia 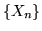 una successione
di var.al. indipendenti aventi la stessa densità. Se esiste la media
una successione
di var.al. indipendenti aventi la stessa densità. Se esiste la media ![$\mu =
E[X_k]$](img524.gif) , allora vale la legge forte dei grandi numeri, cioè
, allora vale la legge forte dei grandi numeri, cioè
per ogni 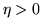 è nulla la probabilità che si verifichino
simultaneamente infinite disuguaglianze del tipo
è nulla la probabilità che si verifichino
simultaneamente infinite disuguaglianze del tipo
Si osservi che non si richiede che le var.al. 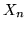 abbiano varianza finita.
abbiano varianza finita.
Quando esiste la varianza delle 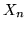 vale un risultato molto più forte (il
Teorema Limite Centrale).
vale un risultato molto più forte (il
Teorema Limite Centrale).
Definizione. Si chiama distribuzione normale la funzione 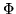 definita
da
definita
da
Ricordiamo che come si sa dall'analisi
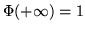 e naturalmente
e naturalmente
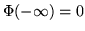 ; inoltre
; inoltre
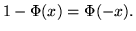
Possiamo ora enunciare il
Teorema 3.2.3 (Teorema Limite Centrale). Sia  una successione
di var.al. indipendenti aventi la stessa densità. Supponiamo che esistano la
media
una successione
di var.al. indipendenti aventi la stessa densità. Supponiamo che esistano la
media ![$\mu =
E[X_k]$](img524.gif) , e la varianza
, e la varianza
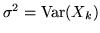 . Allora, posto
. Allora, posto
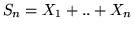 , qualunque sia
, qualunque sia 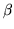 si ha
si ha
Tratteremo la dimostrazione di questo teorema nel capitolo sulla probabilità nel
continuo.
Osserviamo intanto che per 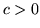 si ha
si ha
Pertanto, applicando la (1), si ottiene
Mostriamo ora che, se 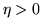 , per ogni funzione
, per ogni funzione 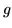 tale che
tale che
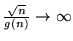 per
per
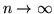 , si ha
, si ha
che è un risultato ben più forte della legge debole. Si ha infatti
quest'ultima probabilità è definitivamente minore o uguale di
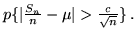 Si ha quindi
Si ha quindi
da cui, facendo tendere 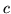 a
a 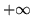 e ricordando che
e ricordando che
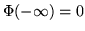 , segue
la (2).
, segue
la (2).



Next: Esercizi e complementi
Up: La legge dei grandi
Previous: La legge debole
Stefani Gianna
2000-11-06
![]() la disuguaglianza di Kolmogorov si riduce alla
disuguaglianza di Chebyshev. In effetti basta prendere
la disuguaglianza di Kolmogorov si riduce alla
disuguaglianza di Chebyshev. In effetti basta prendere
![]()
![]() e la stessa varianza
e la stessa varianza ![]() , allora
con la scelta di
, allora
con la scelta di
![]() in luogo delle
in luogo delle ![]() disuguaglianze
(*) si hanno le
disuguaglianze
(*) si hanno le ![]() disuguaglianze
disuguaglianze
![]() .
Indichiamo con
.
Indichiamo con ![]() il numero di successi nelle
il numero di successi nelle ![]() prove. La nozione intuitiva di
probabilità vorrebbe che per la frequenza di successi
prove. La nozione intuitiva di
probabilità vorrebbe che per la frequenza di successi ![]() si avesse
si avesse
![]() : in effetti questo evento si verifica con
probabilità 1, ma la questione andrebbe trattata con la probabilità nel
continuo. Comunque questo risultato non è contenuto nella legge debole (ma
in quella forte). La legge debole afferma che
: in effetti questo evento si verifica con
probabilità 1, ma la questione andrebbe trattata con la probabilità nel
continuo. Comunque questo risultato non è contenuto nella legge debole (ma
in quella forte). La legge debole afferma che