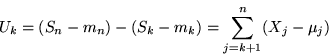Next: La probabilità nel continuo
Up: La legge dei grandi
Previous: La legge forte
1. Dimostrazione della legge debole.
Sia  la densità delle
la densità delle 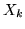 . Non è restrittivo
supporre
. Non è restrittivo
supporre 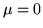 . Fissato
. Fissato  ,
per ogni
,
per ogni  definiamo
definiamo  coppie di var.al.
coppie di var.al.
Si ha evidentemente che
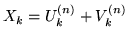 .
.
Per provare la (*) basterà mostrare che, dato
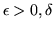 può
essere scelto in modo che per
può
essere scelto in modo che per
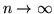
Sia ![$a = E[\vert X_k\vert]$](img589.gif) , allora (omettendo l'indice
, allora (omettendo l'indice  in alto)
in alto)
Le 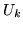 sono var.al. indipendenti e con la stessa distribuzione, si ha quindi
sono var.al. indipendenti e con la stessa distribuzione, si ha quindi
Si osservi che per
![$n \rightarrow \infty, E[U_1] \rightarrow E[X_1] = 0$](img593.gif) per cui per
per cui per
 abbastanza grande:
abbastanza grande:
Se ora applichiamo la disuguaglianza di Chebyshev otteniamo:
siccome 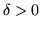 è arbitrario, questa implica la prima delle (**). Per
quanto riguarda la seconda delle (**) osserviamo che si ha
è arbitrario, questa implica la prima delle (**). Per
quanto riguarda la seconda delle (**) osserviamo che si ha
l'ultima somma tende a zero se  tende all'infinito e quindi la dimostrazione è
completa.
tende all'infinito e quindi la dimostrazione è
completa.
2. Dimostrazione della disuguaglianza di Kolmogorov.
Poniamo 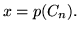 Per
Per 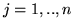 definiamo var.al.
definiamo var.al. 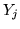 nel seguente modo:
nel seguente modo: 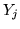 vale 1 nei punti in cui la j-ma è la prima delle
disuguaglianze (*) ad essere soddisfatta, vale 0 altrimenti. Dunque
vale 1 nei punti in cui la j-ma è la prima delle
disuguaglianze (*) ad essere soddisfatta, vale 0 altrimenti. Dunque 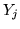 vale 1
se
vale 1
se
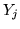 vale 0 in ogni altro caso. Pertanto in ogni punto al più una delle
vale 0 in ogni altro caso. Pertanto in ogni punto al più una delle 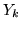 vale 1 e quindi la somma
vale 1 e quindi la somma 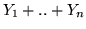 prende solo i valori 0 e 1; vale 1 se e solo
se una almeno delle disuguaglianze (*) è soddisfatta; questo significa che
prende solo i valori 0 e 1; vale 1 se e solo
se una almeno delle disuguaglianze (*) è soddisfatta; questo significa che
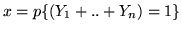 . Dalla disuguaglianza
. Dalla disuguaglianza
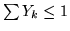 moltiplicando per
moltiplicando per
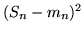 e prendendo la media
e prendendo la media 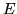 si ottiene
si ottiene
Stimeremo ora il primo membro di questa disuguaglianza. Ponendo
si ottiene
Notiamo che 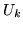 dipende solo da
dipende solo da
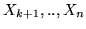 mentre
mentre 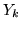 e
e 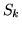 solo da
solo da
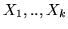 ; pertanto
; pertanto 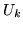 è indipendente da
è indipendente da
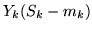 .
Tenendo conto che
.
Tenendo conto che ![$E[U_k] = 0$](img615.gif) , otteniamo
, otteniamo
Questo implica che
![$E[Y_k(S_n - m_n)^2] \geq E[Y_k(S_k - m_k)^2]$](img617.gif) . D'altra
parte
. D'altra
parte 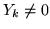 solo se
solo se
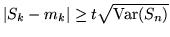 per cui
per cui
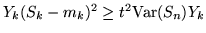 . Possiamo quindi concludere che
. Possiamo quindi concludere che
ossia
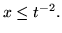



Next: La probabilità nel continuo
Up: La legge dei grandi
Previous: La legge forte
Stefani Gianna
2000-11-06
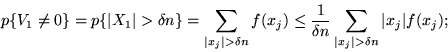
![\begin{displaymath}\sum_{k=1}^n E[Y_k(S_n - m_n)^2] \leq E[(S_n - m_n)^2] =
{\rm Var}(S_n)\,.\end{displaymath}](img608.gif)