Next: La legge forte
Up: La legge dei grandi
Previous: La legge dei grandi
Teorema 3.1.1 (Legge debole dei grandi numeri). Sia 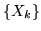 una successione
di var.al. indipendenti aventi la stessa densità. Se esiste la media
una successione
di var.al. indipendenti aventi la stessa densità. Se esiste la media ![$\mu =
E[X_k]$](img524.gif) , allora qualunque sia
, allora qualunque sia 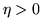 si ha
si ha
(Per la dimostrazione di questo teorema vedi appendice del capitolo). Conviene qui
premettere qualche osservazione. Poniamo
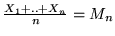 : il teorema afferma che
: il teorema afferma che
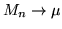 secondo
un certo tipo di convergenza per var.al. (che poi sono funzioni). Nel linguaggio
della teoria delle funzioni reali questa convergenza viene chiamata convergenza
in misura o anche convergenza in probabilità. In realtà le ipotesi di
questo teorema implicano una convergenza più forte, la convergenza quasi
ovunque (per funzioni): vale cioè, come vedremo, una ``legge forte dei grandi
numeri".
secondo
un certo tipo di convergenza per var.al. (che poi sono funzioni). Nel linguaggio
della teoria delle funzioni reali questa convergenza viene chiamata convergenza
in misura o anche convergenza in probabilità. In realtà le ipotesi di
questo teorema implicano una convergenza più forte, la convergenza quasi
ovunque (per funzioni): vale cioè, come vedremo, una ``legge forte dei grandi
numeri".
Se aggiungiamo un'ipotesi speciale, cioè che esistano le varianze
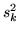 delle
delle 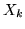 , il teorema ammette una dimostrazione molto semplice e per
altri versi più generale (non occorre supporre che le
, il teorema ammette una dimostrazione molto semplice e per
altri versi più generale (non occorre supporre che le 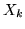 abbiano la stessa
densità) che qui riportiamo .
abbiano la stessa
densità) che qui riportiamo .
Teorema (Legge debole dei grandi numeri in ipotesi di varianza).
Sia 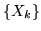 una successione di var.al. indipendenti di media
una successione di var.al. indipendenti di media 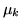 e di
varianza
e di
varianza 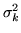 . Poniamo
. Poniamo
allora, se
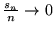 , per ogni
, per ogni 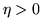 si ha
si ha
Dimostrazione. Applicando la disuguaglianza di Chebyshev si ha
e l'ultimo termine è infinitesimo.



Next: La legge forte
Up: La legge dei grandi
Previous: La legge dei grandi
Stefani Gianna
2000-11-06