


Next: Esercizi e complementi
Up: Variabili aleatorie.
Previous: Esempi
Sia  una var.al. che
prende valori interi positivi, per ogni
una var.al. che
prende valori interi positivi, per ogni 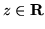 poniamo
poniamo
Definizione 2.8.1. La funzione 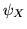 si chiama funzione generatrice
delle probabilità.
si chiama funzione generatrice
delle probabilità.
Se 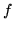 è la densità di
è la densità di  , per il Teorema 2.5.1, si ha
, per il Teorema 2.5.1, si ha
Questa serie di potenze ha raggio di convergenza 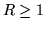 (perchè
(perchè
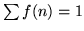 ),
), 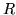 può anche essere +
può anche essere +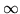 , come nel caso che
, come nel caso che  prenda
solo un insieme finito di valori e
prenda
solo un insieme finito di valori e 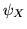 si riduce a un polinomio.
si riduce a un polinomio.
Si vede facilmente che due var.al. a valori interi positivi hanno la stessa
densità se e solo se hanno la stessa funzione generatrice. Se la funzione
generatrice di  è data in forma esplicita (non come serie), la densità di
è data in forma esplicita (non come serie), la densità di  si calcola con
derivazioni successive nell'origine. Diamo subito alcuni esempi
si calcola con
derivazioni successive nell'origine. Diamo subito alcuni esempi
Binomiale. Sia  una var.al.
una var.al. 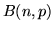 , si ha
, si ha
Poisson . Sia  una var.al. che segue la legge di Poisson di
parametro
una var.al. che segue la legge di Poisson di
parametro 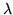 , si ha
, si ha
Risulta molto utile il
Teorema 2.8.1. Siano  e
e 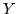 var.al. indipendenti. Allora
var.al. indipendenti. Allora
Dimostrazione. Per il Teorema 2.3.1 anche 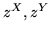 sono var.al. indipendenti,
pertanto si ha
sono var.al. indipendenti,
pertanto si ha
Questo teorema può essere usato per calcolare la densità della somma di due
var.al. come si vede nel seguente esempio.
Somma di geometriche. Siano  e
e 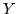 due var.al. indipendenti di densità
geometrica
due var.al. indipendenti di densità
geometrica
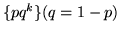 . La loro funzione generatrice vale
. La loro funzione generatrice vale
Se 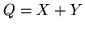 si ha
si ha
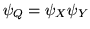 ossia
ossia
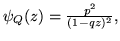 con facili
calcoli si ha poi
con facili
calcoli si ha poi
e quindi per la densità di 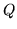 si ottiene
si ottiene
Mostriamo anche il
Teorema 2.8.2. Se la serie che definisce la funzione generatrice 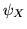 ha raggio di convergenza
ha raggio di convergenza 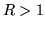 , allora la var.al.
, allora la var.al.  ha momenti di ogni ordine;
in particolare
ha momenti di ogni ordine;
in particolare
Dimostrazione. Derivando 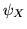 e valutando in 1 si ottiene
e valutando in 1 si ottiene
derivando una seconda volta e valutando in 1 si ottiene
da cui segue subito la formula per la varianza. Allo stesso modo (con derivate
successive) si possono determinare i momenti di ordine maggiore.



Next: Esercizi e complementi
Up: Variabili aleatorie.
Previous: Esempi
Stefani Gianna
2000-11-06
![]() è la densità di
è la densità di ![]() , per il Teorema 2.5.1, si ha
, per il Teorema 2.5.1, si ha
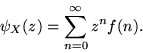
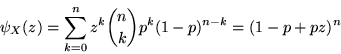
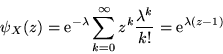
![]() e
e ![]() var.al. indipendenti. Allora
var.al. indipendenti. Allora
![]() e
e ![]() due var.al. indipendenti di densità
geometrica
due var.al. indipendenti di densità
geometrica
![]() . La loro funzione generatrice vale
. La loro funzione generatrice vale
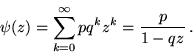
![\begin{displaymath}\psi_X'(1) = \sum_{k=1}^\infty kf(k) = E[X];\end{displaymath}](img481.gif)
![\begin{displaymath}\psi_X''(1) = \sum_{k=1}^\infty (k^2-k)f(k) = E[X^2]-E[X]\end{displaymath}](img482.gif)