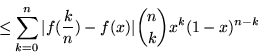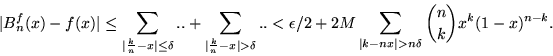Next: La legge dei grandi
Up: Variabili aleatorie.
Previous: Funzioni generatrici
1. Il problema del collezionista.
Una popolazione contiene  elementi distinti, tutti in ugual proporzione, (ad es.
figurine per una collezione). Si fanno estrazioni con rimpiazzo. Un campione di
dimensione
elementi distinti, tutti in ugual proporzione, (ad es.
figurine per una collezione). Si fanno estrazioni con rimpiazzo. Un campione di
dimensione 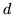 in generale conterrà meno di
in generale conterrà meno di 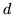 elementi distinti a causa delle
ripetizioni (i doppioni). Sia
elementi distinti a causa delle
ripetizioni (i doppioni). Sia 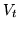 la var.al. ``numero di estrazioni necessarie per
avere
la var.al. ``numero di estrazioni necessarie per
avere 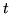 elementi distinti"; i valori possibili per
elementi distinti"; i valori possibili per 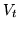 sono
sono 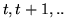 . Si
vuole calcolare la media di
. Si
vuole calcolare la media di 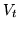 .
.
Soluzione.
Diciamo che un'estrazione ha successo se risulta nell'aggiunta di un nuovo elemento
nel campione. Poniamo poi
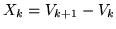 ; allora
; allora 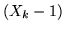 è il
numero di estrazioni con insuccesso tra il
è il
numero di estrazioni con insuccesso tra il  -mo successo e il
-mo successo e il 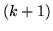 -mo
successo. Durante tutte queste estrazioni la popolazione contiene
-mo
successo. Durante tutte queste estrazioni la popolazione contiene 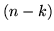 elementi
che non sono entrati nel campione, per cui
elementi
che non sono entrati nel campione, per cui 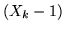 è il numero di insuccessi
che precedono il primo successo in prove ripetute di Bernoulli con
è il numero di insuccessi
che precedono il primo successo in prove ripetute di Bernoulli con
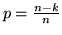 .
. 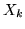 prende il valore
prende il valore 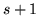 con probabilità
con probabilità 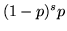 per
cui, facendo i calcoli, si ottiene
per
cui, facendo i calcoli, si ottiene
![$E[X_k] = \frac{1}{p} = \frac{n-k}{n}$](img493.gif) . Si noti
ora che
. Si noti
ora che
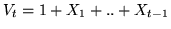 , per cui
, per cui
In particolare
![$E[V_n] \simeq n \log n$](img496.gif) e (assumendo
e (assumendo  pari)
pari)
![$E[V_{n/2}] \simeq n \log 2$](img497.gif) . Si osservi come il numero atteso di prove per
completare la collezione sia in generale assai più grande del doppio del
numero atteso di prove per completare metà collezione.
. Si osservi come il numero atteso di prove per
completare la collezione sia in generale assai più grande del doppio del
numero atteso di prove per completare metà collezione.
2. Varianza di somme.
Supponiamo che  var.al.
var.al. 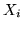 abbiano varianza finita, allora per la varianza
della loro somma si ha la formula generale
abbiano varianza finita, allora per la varianza
della loro somma si ha la formula generale
3. Problema dei matches
Facciamo riferimento a 2 di 1.4 . Sia 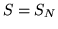 la var.al.
``numero di matches", si
chiedono la media e la varianza di
la var.al.
``numero di matches", si
chiedono la media e la varianza di 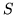 .
.
Soluzione.
Sia 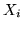 la var.al. che vale 1 (con probab.
la var.al. che vale 1 (con probab. 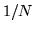 ) se all'i-mo posto c'è match
e 0 altrimenti. Abbiamo
) se all'i-mo posto c'è match
e 0 altrimenti. Abbiamo
Calcoliamo le covarianze. Per 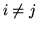 la var.al
la var.al 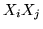 prende solo valori 0 e
1, quest'ultimo con prob.
prende solo valori 0 e
1, quest'ultimo con prob.
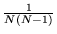 . Pertanto si ha
. Pertanto si ha
Applicando la formula (*) si ottiene
4. Polinomi di Bernstein
Diamo ora una interessante applicazione dei metodi probabilistici alla teoria
dell'approssimazione.
Sia  una funzione reale continua su
una funzione reale continua su ![$[0,1]$](img507.gif) , per
, per
![$n \in {\bf N},\;
x \in [0,1]$](img508.gif) ; l'
; l' -mo polinomio di Bernstein della
-mo polinomio di Bernstein della  è definito da
è definito da
Faremo vedere che 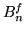 converge uniformemente a
converge uniformemente a  ; dando così
una dimostrazione del teorema di Weierstrass: ``I polinomi sono densi nello spazio
delle funzioni continue". Si ha
; dando così
una dimostrazione del teorema di Weierstrass: ``I polinomi sono densi nello spazio
delle funzioni continue". Si ha
Poichè  è uniformemente continua, fissato
è uniformemente continua, fissato 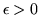 esiste un
esiste un
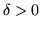 tale che:
tale che:
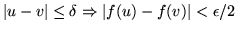 ;
sia poi
;
sia poi 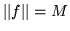 . Si ha
. Si ha
Se si interpreta 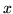 come la probabilità parametro di una var.al.
come la probabilità parametro di una var.al. 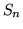 binomiale
(avente media
binomiale
(avente media 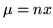 ), allora l'ultima somma eguaglia
), allora l'ultima somma eguaglia
Questa quantità, usando la disuguaglianza
di Chebyshev, si maggiora con
Otteniamo
dunque
e quindi
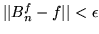 per
per  sufficientemente grande.
sufficientemente grande.



Next: La legge dei grandi
Up: Variabili aleatorie.
Previous: Funzioni generatrici
Stefani Gianna
2000-11-06
![]() elementi distinti, tutti in ugual proporzione, (ad es.
figurine per una collezione). Si fanno estrazioni con rimpiazzo. Un campione di
dimensione
elementi distinti, tutti in ugual proporzione, (ad es.
figurine per una collezione). Si fanno estrazioni con rimpiazzo. Un campione di
dimensione ![]() in generale conterrà meno di
in generale conterrà meno di ![]() elementi distinti a causa delle
ripetizioni (i doppioni). Sia
elementi distinti a causa delle
ripetizioni (i doppioni). Sia ![]() la var.al. ``numero di estrazioni necessarie per
avere
la var.al. ``numero di estrazioni necessarie per
avere ![]() elementi distinti"; i valori possibili per
elementi distinti"; i valori possibili per ![]() sono
sono ![]() . Si
vuole calcolare la media di
. Si
vuole calcolare la media di ![]() .
.
![]() ; allora
; allora ![]() è il
numero di estrazioni con insuccesso tra il
è il
numero di estrazioni con insuccesso tra il ![]() -mo successo e il
-mo successo e il ![]() -mo
successo. Durante tutte queste estrazioni la popolazione contiene
-mo
successo. Durante tutte queste estrazioni la popolazione contiene ![]() elementi
che non sono entrati nel campione, per cui
elementi
che non sono entrati nel campione, per cui ![]() è il numero di insuccessi
che precedono il primo successo in prove ripetute di Bernoulli con
è il numero di insuccessi
che precedono il primo successo in prove ripetute di Bernoulli con
![]() .
. ![]() prende il valore
prende il valore ![]() con probabilità
con probabilità ![]() per
cui, facendo i calcoli, si ottiene
per
cui, facendo i calcoli, si ottiene
![]() . Si noti
ora che
. Si noti
ora che
![]() , per cui
, per cui
![\begin{displaymath}E[V_t] = n \,( \frac{1}{n} + \frac{1}{n-1} + ..+ \frac{1}{n-t...
...t+1/2}^{n+1/2} \frac{1}{x} dx = n \log \frac{n+1/2}{n-t+1/2}\,.\end{displaymath}](img495.gif)
![\begin{displaymath}E[X_i] = 1/N,\; S = \sum_{i=1}^N X_i ,\; E[S] = 1,\;{\rm Var}(X_i) = (N-1)/N^2
\,.\end{displaymath}](img501.gif)
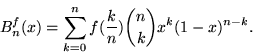
![\begin{displaymath}\vert B_n^f(x) - f(x)\vert = \vert\sum_{k=0}^n [f(\frac{k}{n})-f(x)] {n\choose k} x^k
(1-x)^{n-k}\vert \leq \end{displaymath}](img511.gif)