


Next: Funzioni generatrici
Up: Variabili aleatorie.
Previous: Momenti, varianza
1. Schema di Bernoulli. Siano 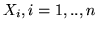 le var.al. di legge
le var.al. di legge
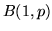 relative alle prove successive in uno schema di Bernoulli.
Le
relative alle prove successive in uno schema di Bernoulli.
Le 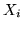 sono indipendenti. Per ogni
sono indipendenti. Per ogni 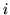 si ha
si ha
![$E[X_i] = 1p + 0(1-p) = p$](img395.gif) e quindi
e quindi ![$E[S_n] = np$](img396.gif) dove
dove
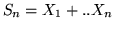 .
.
Si noti che abbiamo calcolato la media di 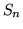 senza bisogno di conoscere la sua
densità
senza bisogno di conoscere la sua
densità 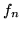 . Questa come sappiamo (Teorema 2.1.1) è
. Questa come sappiamo (Teorema 2.1.1) è
Si ha poi
![${\rm Var}(X_i) = E[X_i^2] - E[X_i]^2 = p - p^2 = p(1-p)$](img400.gif) e di conseguenza
e di conseguenza
La disuguaglianza di Chebyshev ci dice
ovvero, considerando la frequenza 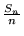 dei successi
nelle
dei successi
nelle  prove,
prove,
Se scegliamo
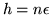 in questa disuguaglianza si ottiene
in questa disuguaglianza si ottiene
in particolare se il numero  delle prove tende all'infinito, tende a zero
la probabilità di una deviazione della frequenza
delle prove tende all'infinito, tende a zero
la probabilità di una deviazione della frequenza 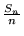 dei successi
dalla probabilità
dei successi
dalla probabilità 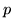 di successo in ogni singola prova. Questo è un caso
particolare della legge (debole) dei grandi numeri. Questo giustifica il metodo di
osservare la frequenza di un risultato per stabilirne la probabilità.
di successo in ogni singola prova. Questo è un caso
particolare della legge (debole) dei grandi numeri. Questo giustifica il metodo di
osservare la frequenza di un risultato per stabilirne la probabilità.
2. Densità di Poisson.
Si chiama distribuzione di Poisson di parametro
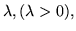 la densità
la densità
La densità di Poisson si può vedere come un'approssimazione di una
densità binomiale 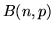 con
con  grande e
grande e 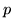 piccolo. Siano dunque
piccolo. Siano dunque 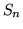 var.al. con densità binomiale
var.al. con densità binomiale
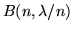 , si ha:
, si ha:
se si fa tendere  all'
all'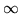 si vede, con facili
calcoli, che
si vede, con facili
calcoli, che
inoltre la convergenza è uniforme rispetto a  .
.
La distribuzione di Poisson è detta anche legge degli eventi rari, infatti si
presenta come legge di una var.al. 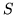 che rappresenta il numero di successi su un
numero molto grande di prove ripetute indipendenti, in ciascuna delle quali
la probabilità di successo è molto piccola.
che rappresenta il numero di successi su un
numero molto grande di prove ripetute indipendenti, in ciascuna delle quali
la probabilità di successo è molto piccola.
Siano  e
e 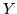 due var.al. indipendenti di Poisson di parametri
due var.al. indipendenti di Poisson di parametri
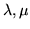 e di densità
e di densità 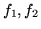 resp.; vogliamo trovare la densità
resp.; vogliamo trovare la densità
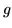 della somma
della somma 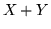 . Si ha, ricordando che
. Si ha, ricordando che 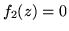 se
se 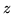 è negativo,
è negativo,
Dunque 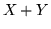 è di Poisson con parametro
è di Poisson con parametro
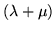 .
.
Sia  una var.al. con densità di Poisson di parametro
una var.al. con densità di Poisson di parametro
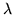 , si ha
, si ha
3. Distribuzione ipergeometrica. Un'urna contiene
 palline di cui
palline di cui 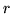 rosse (
rosse (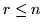 ); se ne estraggono (senza rimpiazzo)
); se ne estraggono (senza rimpiazzo)
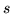 (
(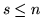 ); la var.al.
); la var.al.  che dà il numero di palline rosse estratte
ha la densità ipergeometrica
che dà il numero di palline rosse estratte
ha la densità ipergeometrica
Anche in questo caso per calcolare ![$E[X]$](img422.gif) non abbiamo bisogno di conoscere la
densità. Possiamo ragioniare così: sia
non abbiamo bisogno di conoscere la
densità. Possiamo ragioniare così: sia 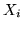 la var.al. che vale 1 se
nell'i-esima estrazione viene una pallina rossa e 0 altrimenti. Sono state estratte
la var.al. che vale 1 se
nell'i-esima estrazione viene una pallina rossa e 0 altrimenti. Sono state estratte
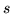 palline, essendoci simmetria (non ci sono palline privilegiate nel gruppo
estratto) ogni pallina ha la stessa probabilità di essere rossa per esempio
quella della prima estratta. Al primo colpo la probabilità di successo di
palline, essendoci simmetria (non ci sono palline privilegiate nel gruppo
estratto) ogni pallina ha la stessa probabilità di essere rossa per esempio
quella della prima estratta. Al primo colpo la probabilità di successo di 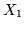 vale
vale 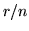 , per cui per ogni
, per cui per ogni 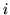 si ha
si ha
![$E[X_i] = (r/n)1 + (1-r/n)0$](img425.gif) . Pertanto
. Pertanto
![$E[X] =
\sum E[X_i] = s(r/n)$](img426.gif) . Si osservi che essendo
. Si osservi che essendo 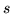 il numero di estrazioni ed
avendo ogni estrazione la stessa probabilità
il numero di estrazioni ed
avendo ogni estrazione la stessa probabilità 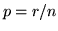 di successo, la
var.al
di successo, la
var.al  si comporta per quanto riguarda il calcolo della media come se
fosse binomiale e questo nonostante che le var.al
si comporta per quanto riguarda il calcolo della media come se
fosse binomiale e questo nonostante che le var.al 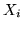 non siano
indipendenti.
non siano
indipendenti.
4. Densità geometrica. Consideriamo sempre prove
ripetute con probabilità
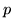 di successo. Problema: determinare la probabilità che ci vogliano esattamente
di successo. Problema: determinare la probabilità che ci vogliano esattamente
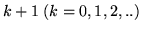 lanci per ottenere il (primo) successo. Si ha successo esattamente al
lanci per ottenere il (primo) successo. Si ha successo esattamente al
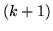 -mo lancio se e solo se si è verificata la sequenza
-mo lancio se e solo se si è verificata la sequenza
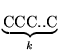 T; questa ha probabilità
T; questa ha probabilità
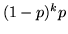 . Si chiama densità geometrica di parametro
. Si chiama densità geometrica di parametro 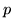 la densità
la densità
Sia 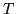 la var.al. ``numero di lanci necessari per il primo successo", allora
la var.al. ``numero di lanci necessari per il primo successo", allora  è la densità di
è la densità di 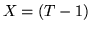 . Si ha:
. Si ha:
Mostriamo ora la ``mancanza di memoria" della legge geometrica. Cominciamo ad
osservare che
Calcoliamo adesso una probabilità condizionale:
Applichiamo questi risultati alla var.al. 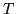 : supponiamo di non aver avuto alcun
successo nelle prime
: supponiamo di non aver avuto alcun
successo nelle prime  prove: qual'è la probabilità di dover attendere
ancora
prove: qual'è la probabilità di dover attendere
ancora 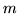 prove? Risposta: la stessa che si avrebbe ricominciando da capo le prove.
Questo spiega l'espressione ``mancanza di memoria".
prove? Risposta: la stessa che si avrebbe ricominciando da capo le prove.
Questo spiega l'espressione ``mancanza di memoria".
Se diamo credito a questo modello probabilistico, allora la pratica diffusa di
giocare al lotto i numeri ``ritardatari" non è giustificata.
5. Distribuzione binomiale negativa.
Si generalizza l'esempio precedente nel seguente modo: consideriamo una sequenza di
prove di Bernoulli con probabilità di successo 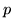 e di insuccesso
e di insuccesso 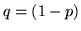 , ci si chiede quanto si deve aspettare per l'
, ci si chiede quanto si deve aspettare per l'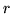 -mo successo. Per il numero
-mo successo. Per il numero
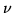 di prove necessarie sarà
di prove necessarie sarà 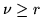 scriviamo
scriviamo 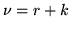 . Indicheremo
con
. Indicheremo
con 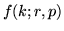 la probabilità che l'
la probabilità che l'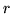 -mo successo avvenga alla prova
-mo successo avvenga alla prova
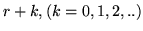 ; ovvero la probabilità che esattamente
; ovvero la probabilità che esattamente  insuccessi precedano
l'
insuccessi precedano
l'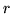 -mo successo. Ciò avviene se e solo se tra le prime (r+k-1) prove ci sono
-mo successo. Ciò avviene se e solo se tra le prime (r+k-1) prove ci sono
 insuccessi e la seguente è un successo; pertanto avremo
insuccessi e la seguente è un successo; pertanto avremo
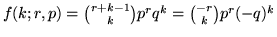 . (Si ricordi che
. (Si ricordi che
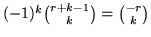 ). Chiameremo distribuzione binomiale
negativa di parametri
). Chiameremo distribuzione binomiale
negativa di parametri 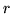 e
e 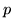 la densità
la densità
Ricordando lo sviluppo in serie binomiale di 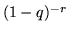 si verifica, come deve
essere, che
si verifica, come deve
essere, che
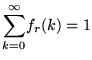 .
Si osservi che per
.
Si osservi che per 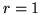 la densità binomiale negativa si riduce alla
densità geometrica.
la densità binomiale negativa si riduce alla
densità geometrica.
Non è difficile calcolare la media di una binomiale negativa usando la
densità in base alla definizione; ma è più istruttivo procedere nel
modo seguente:
sia 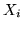 la var.al. che indica il numero di insuccessi che ci sono tra l'
la var.al. che indica il numero di insuccessi che ci sono tra l'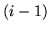 -mo
e l'
-mo
e l'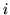 -mo successo. Qualunque sia
-mo successo. Qualunque sia 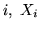 ha densità geometrica
ha densità geometrica
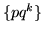 e media
e media ![$E[X_i] = q/p$](img454.gif) . La var.al.
. La var.al.
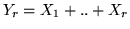 rappresenta il numero di insuccessi che precedo l'
rappresenta il numero di insuccessi che precedo l'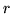 -mo successo e quindi ha
densità
-mo successo e quindi ha
densità 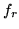 . Siccome
. Siccome
![$E[Y_r] = \sum E[X_i]$](img457.gif) , si ottiene
, si ottiene ![$E[Y_r]=r q/p$](img458.gif) .
.



Next: Funzioni generatrici
Up: Variabili aleatorie.
Previous: Momenti, varianza
Stefani Gianna
2000-11-06
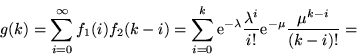
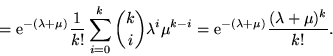

 T; questa ha probabilità
T; questa ha probabilità
![\begin{displaymath}E[X] = \sum_{k=0}^\infty kp(1-p)^k = \frac{1-p}{p},\end{displaymath}](img434.gif)
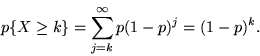
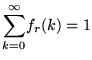 .
Si osservi che per
.
Si osservi che per