


Next: Esempi
Up: Variabili aleatorie.
Previous: Speranza matematica
Definizione 2.6.1. Sia  una var.al.; diremo che
una var.al.; diremo che  ha momento di
ordine
ha momento di
ordine  finito (
finito (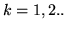 ) se
) se 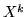 ha media finita. In questo caso
ha media finita. In questo caso
![$E[X^k]$](img359.gif) si chiama momento di ordine
si chiama momento di ordine  della var.al.
della var.al.  . Se
. Se
![$(X-E[X])^k$](img360.gif) ha media finita diremo che
ha media finita diremo che  ha momento centrato di
ordine
ha momento centrato di
ordine  finito e chiameremo
finito e chiameremo ![$E[(X-E[X])^k]$](img361.gif) momento centrato di
ordine
momento centrato di
ordine  di
di  .
.
Applicando il Teorema 2.5.1, indicando con 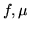 risp. la densità e la
media di
risp. la densità e la
media di  otteniamo:
otteniamo:
Teorema 2.6.1. i) Se  ha momento finito di ordine
ha momento finito di ordine  , allora ha anche momento
finito di ordine
, allora ha anche momento
finito di ordine 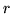 per ogni
per ogni 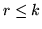 .
.
ii) Se  e
e 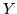 hanno momento finito
di ordine
hanno momento finito
di ordine
 , allora anche
, allora anche 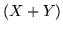 ha momento finito di ordine
ha momento finito di ordine  . In particolare se
. In particolare se  ha
momento finito di ordine
ha
momento finito di ordine  , allora ha anche momento centrato finito di ordine
, allora ha anche momento centrato finito di ordine  .
.
Dimostrazione . Siano 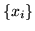 i valori assunti da
i valori assunti da  , per ogni
, per ogni 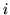 si ha
si ha
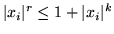 e di conseguenza
e di conseguenza
pertanto la serie che definisce il momento di ordine  converge assolutamente per
il criterio del confronto. Questo prova i). Per quanto riguarda la ii) basta
osservare che, per la convessità della funzione
converge assolutamente per
il criterio del confronto. Questo prova i). Per quanto riguarda la ii) basta
osservare che, per la convessità della funzione 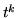 , si ha la disuguaglianza:
, si ha la disuguaglianza:
Di particolare importanza è il momento centrato di
ordine 2 che viene chiamato varianza:
Per quanto elementare il teorema che segue si rivela estremamente utile
in molte circostanze:
Teorema 2.6.2 (disuguaglianza di Chebyshev). Se per la var.al.  esiste il momento
esiste il momento ![$E[X^2]$](img370.gif) (e di conseguenza la varianza) per ogni
(e di conseguenza la varianza) per ogni
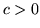 si ha:
si ha:
in particolare, posto ![$\mu = E[X]$](img373.gif) ,
,
Dimostrazione. Applicando la prima disuguaglianza alla var.al. 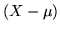 , si
deduce la seconda. Si noti ora che
, si
deduce la seconda. Si noti ora che
si ha poi
Fissata la var.al.  , di solito media e varianza si denotano risp. con
, di solito media e varianza si denotano risp. con
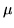 e
e 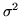 ;
;
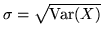 si chiama deviazione
standard di
si chiama deviazione
standard di  . Se
. Se  e
e 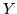 hanno varianza finita, è finita anche la
quantità
hanno varianza finita, è finita anche la
quantità
![$E[(X-\mu_X)(Y-\mu_Y)]$](img381.gif) che si chiama covarianza di
che si chiama covarianza di  e
e 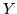 e si
indica con
e si
indica con
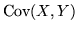 .
.
Si provano facilmente le seguenti proprietà:
i)
![${\rm Var}(X) = E[X^2] - E[X]^2 $](img383.gif) ;
;
ii)
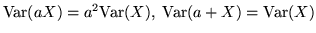 ;
;
iii)
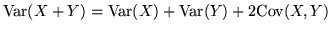 ;
;
iv)
![${\rm Cov}(X,Y) = E[XY] - E[X]E[Y]$](img386.gif) .
.
Se  e
e 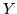 sono indipendenti, applicando il Corollario 2.5.1 iii) si ha
sono indipendenti, applicando il Corollario 2.5.1 iii) si ha
Per quanto visto, la covarianza misura in un certo senso
l'indipendenza delle var.al.; tuttavia può capitare che
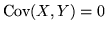 senza che
senza che  e
e 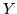 siano indipendenti. Quando
siano indipendenti. Quando
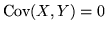 si dice che le
var.al.
si dice che le
var.al.  e
e 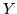 non sono correlate. Si definisce pertanto il
coefficiente di correlazione
non sono correlate. Si definisce pertanto il
coefficiente di correlazione 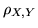 mediante
mediante
Vogliamo provare che
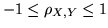 . Per questo notiamo che si ha
sempre
. Per questo notiamo che si ha
sempre
![$E[XY]^2 \leq E[X^2]E[Y^2]$](img392.gif) (si vede col segno di un trinomio); basta
poi applicare la disuguaglianza alle var.al.
(si vede col segno di un trinomio); basta
poi applicare la disuguaglianza alle var.al.
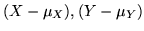 .
.



Next: Esempi
Up: Variabili aleatorie.
Previous: Speranza matematica
Stefani Gianna
2000-11-06
![]() risp. la densità e la
media di
risp. la densità e la
media di ![]() otteniamo:
otteniamo:
![\begin{displaymath}\sum_{\vert x_i\vert>c} f(x_i) = \sum_{\vert x_i\vert>c} f(x_...
..._i^2} \leq \sum_i \frac{f(x_i)x_i^2}{c^2}
= \frac{E[X^2]}{c^2}.\end{displaymath}](img377.gif)
![]() , di solito media e varianza si denotano risp. con
, di solito media e varianza si denotano risp. con
![]() e
e ![]() ;
;
![]() si chiama deviazione
standard di
si chiama deviazione
standard di ![]() . Se
. Se ![]() e
e ![]() hanno varianza finita, è finita anche la
quantità
hanno varianza finita, è finita anche la
quantità
![]() che si chiama covarianza di
che si chiama covarianza di ![]() e
e ![]() e si
indica con
e si
indica con
![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
![]() e
e ![]() sono indipendenti, applicando il Corollario 2.5.1 iii) si ha
sono indipendenti, applicando il Corollario 2.5.1 iii) si ha
![]() senza che
senza che ![]() e
e ![]() siano indipendenti. Quando
siano indipendenti. Quando
![]() si dice che le
var.al.
si dice che le
var.al. ![]() e
e ![]() non sono correlate. Si definisce pertanto il
coefficiente di correlazione
non sono correlate. Si definisce pertanto il
coefficiente di correlazione ![]() mediante
mediante