


Next: Momenti, varianza
Up: Variabili aleatorie.
Previous: Densità di una somma
Sia  una var.al.(discreta) che prende valori
una var.al.(discreta) che prende valori 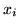 ed ha
densità
ed ha
densità 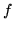 .
.
Definizione 2.5.1. Si dice che  ha speranza matematica
finita se
ha speranza matematica
finita se
in tal caso si chiama speranza matematica (o media o valore atteso)
di  il numero
il numero
se ![$ E[X] = 0$](img316.gif) si dice che la var.al.
si dice che la var.al.  è centrata.
è centrata.
Supponiamo che le var.al.  e
e 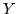 aventi media finita prendano i valori
aventi media finita prendano i valori 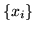 e
e 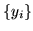 e sia
e sia
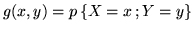 la loro densità
congiunta. Mostriamo che anche la var.al.
la loro densità
congiunta. Mostriamo che anche la var.al. 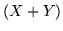 ha media finita. Si ha
ha media finita. Si ha
dove 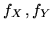 sono le densità marginali di
sono le densità marginali di 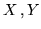 . Con calcoli simili
senza il valore assoluto si prova poi la formula fondamentale
. Con calcoli simili
senza il valore assoluto si prova poi la formula fondamentale
Diamo ora un'importante generalizzazione di questo risultato.
Sia
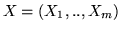 un vettore aleatorio di densità
un vettore aleatorio di densità 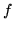 e i cui valori
denoteremo con
e i cui valori
denoteremo con
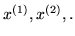 ;
;
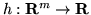 , ponendo
, ponendo 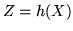 si definisce una nuova var.al.
i cui valori denoteremo con
si definisce una nuova var.al.
i cui valori denoteremo con 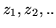 :
:
Teorema 2.5.1. 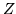 ha speranza matematica finita se e solo se
ha speranza matematica finita se e solo se
e in questo caso
Dimostrazione. Se
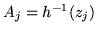 allora
allora
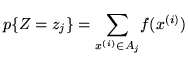 . Abbiamo allora:
. Abbiamo allora:
tenendo conto che se
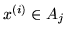 allora
allora
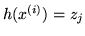
Dunque se la serie
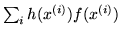 converge assolutamente
converge assolutamente 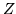 ha speranza matematica finita. La formula per
ha speranza matematica finita. La formula per ![$E[Z]$](img342.gif) si dimostra ripetendo gli
stessi calcoli senza i valori assoluti; si osservi soltanto che il passaggio
si dimostra ripetendo gli
stessi calcoli senza i valori assoluti; si osservi soltanto che il passaggio
che consiste nel sommare riordinando i termini, è lecito
appunto perchè sappiamo che la serie è assolutamente convergente.
Dal teorema precedente, specializzando la funzione 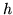 , si deducono come
corollari importanti risultati. Ad esempio
, si deducono come
corollari importanti risultati. Ad esempio
Corollario 2.5.1. Siano  e
e 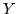 var.al. con media finita.
Allora:
var.al. con media finita.
Allora:
i) 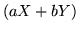 ha media finita e
ha media finita e
![$E[aX + bY] = aE[X]+bE[Y];$](img346.gif)
ii) 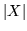 ha media finita e
ha media finita e
![$\vert E[X]\vert \leq E[\vert X\vert];$](img348.gif)
se inoltre  e
e 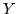 sono indipendenti
sono indipendenti
iii) 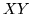 ha media finita e
ha media finita e
![$E[XY] = E[X]E[Y]$](img350.gif)
Dimostrazione. Limitiamoci a provare iii). Siano 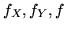 risp.
le densità di
risp.
le densità di 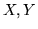 e del vettore
e del vettore 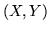 ; per la supposta indipendenza
si ha
; per la supposta indipendenza
si ha
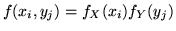 . Applicando il teorema con
. Applicando il teorema con 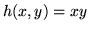 si ottiene
si ottiene
ripetendo gli stessi calcoli senza i valori assoluti si prova che
![$E[XY] = E[X]E[Y]$](img350.gif) .
.



Next: Momenti, varianza
Up: Variabili aleatorie.
Previous: Densità di una somma
Stefani Gianna
2000-11-06
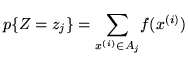 . Abbiamo allora:
. Abbiamo allora:
![]() , si deducono come
corollari importanti risultati. Ad esempio
, si deducono come
corollari importanti risultati. Ad esempio ![]() e
e ![]() var.al. con media finita.
Allora:
var.al. con media finita.
Allora:
![]() ha media finita e
ha media finita e
![]()
![]() ha media finita e
ha media finita e
![]()
![]() e
e ![]() sono indipendenti
sono indipendenti ![]() ha media finita e
ha media finita e
![]()
![]() risp.
le densità di
risp.
le densità di ![]() e del vettore
e del vettore ![]() ; per la supposta indipendenza
si ha
; per la supposta indipendenza
si ha
![]() . Applicando il teorema con
. Applicando il teorema con ![]() si ottiene
si ottiene