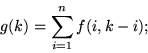Next: Speranza matematica
Up: Variabili aleatorie.
Previous: Variabili aleatorie indipendenti
Consideriamo il problema di calcolare la densità della somma di due var.al.  e
e 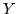 . Si noti che l'evento
. Si noti che l'evento
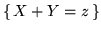 uguaglia l'unione (di eventi
disgiunti)
uguaglia l'unione (di eventi
disgiunti)
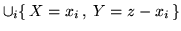 ; risulta quindi chiaro che in
generale per calcolare la densità di una somma non servono le
densità marginali, ma occorre conoscere la densità congiunta del vettore
; risulta quindi chiaro che in
generale per calcolare la densità di una somma non servono le
densità marginali, ma occorre conoscere la densità congiunta del vettore 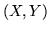 .
.
Teorema 2.4.1. Siano 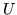 e
e 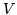 var.al. di densità
congiunta
var.al. di densità
congiunta 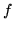 . Allora la densità
. Allora la densità 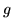 di
di 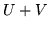 vale
vale
se poi 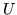 e
e 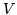 sono indipendenti con densità
sono indipendenti con densità 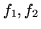 , si ha
, si ha
Dimostrazione. Premettiamo in generale che per ogni var.al. 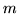 -dimensionale
-dimensionale  di
densità
di
densità 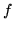 e per ogni
e per ogni
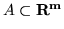 si ha:
si ha:
e se
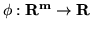
Si usi ora l'ultima formula con 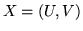 e
e
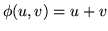 , basta osservare
che
, basta osservare
che 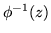 è l'insieme dei vettori
è l'insieme dei vettori 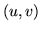 con
con 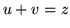 .
.
Teorema 2.4.2. Siano 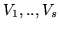 var.al. indipendenti con leggi binomiali
risp.
var.al. indipendenti con leggi binomiali
risp.
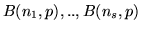 . Allora
. Allora 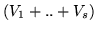 ha legge
ha legge
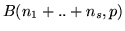 .
.
Dimostrazione. Basta rappresentare 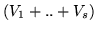 come somma di
come somma di
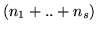 var.al. indipendenti di legge
var.al. indipendenti di legge 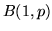 .
.
Esempio 1. Si lanciano 2 dadi a 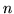 facce, si chiede la probabilità
facce, si chiede la probabilità
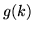 che la somma dei risultati sia esattamente
che la somma dei risultati sia esattamente
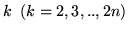 . Si ha
. Si ha
dove
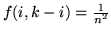 se
se
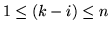 ,
, 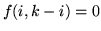 altrimenti.
Pertanto nella sommatoria ci sono
altrimenti.
Pertanto nella sommatoria ci sono 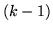 termini non nulli se
termini non nulli se 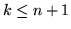 e
e
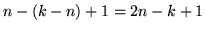 termini non nulli se
termini non nulli se 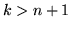 ; si vede quindi che
; si vede quindi che
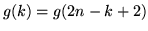 e che per
e che per
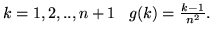



Next: Speranza matematica
Up: Variabili aleatorie.
Previous: Variabili aleatorie indipendenti
Stefani Gianna
2000-11-06